题目内容
平面内有两两相交的4条直线,如果最多有m个交点,最少有n个交点,那么m-n=
- A.3
- B.4
- C.5
- D.6
C
分析:可根据题意,画出图形,找出交点最多和最少的个数,求m-n.
解答:如图所示:



4条直线两两相交,有3种情况:4条直线经过同一点,有一个交点;3条直线经过同一点,被第4条直线所截,有4个交点;4条直线不经过同一点,有6个交点.
故平面内两两相交的4条直线,最多有6个交点,最少有1个交点;即m=6,n=1,则m-n=5.
故选C.
点评:一般地:n条直线相交,最多有1+2+3+…+(n-1)=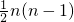 个交点,最少即交点为1个.
个交点,最少即交点为1个.
分析:可根据题意,画出图形,找出交点最多和最少的个数,求m-n.
解答:如图所示:



4条直线两两相交,有3种情况:4条直线经过同一点,有一个交点;3条直线经过同一点,被第4条直线所截,有4个交点;4条直线不经过同一点,有6个交点.
故平面内两两相交的4条直线,最多有6个交点,最少有1个交点;即m=6,n=1,则m-n=5.
故选C.
点评:一般地:n条直线相交,最多有1+2+3+…+(n-1)=
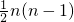 个交点,最少即交点为1个.
个交点,最少即交点为1个. 
练习册系列答案
相关题目