题目内容
【题目】如图,已知正方形ABCD和正方形AEFG,连结BE、DG.
(1)请你判断线段BE和DG的关系并证明你的结论;
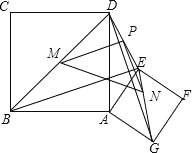
(2)连接BD、EG、DE,点M、N、P分别是BD、EG、DE的中点,连接MP,PN,MN,请你画出图形并判断△MPN的形状,说明理由
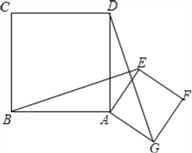
【答案】(1)BE和DG的关系是:BE=DG;BE⊥DG,证明见解析;(2)△MPN是等腰直角三角形,理由见解析
【解析】分析:(1)根据SAS证明△BEA与△DAG全等,再利用全等三角形的性质证明即可;(2)利用三角形中位线定理证得△MPN是等腰直角三角形;
本题解析:
(1)BE和DG的关系是:BE=DG;BE⊥DG
证明:∵正方形ABCD和正方形AEFG, ∴AB=AD,AE=AG,∠BAD=∠EAG=90°,∴∠BAD+∠DAE=∠EAG+∠DAE, ∴∠BAE=∠DAG,
∵在△BEA与△DAG中,
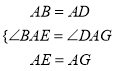
∴△BEA≌△DAG(SAS);∴BE=DG,∠ADG=∠ABE,
∴∠BOD=∠BAD=90°,
∴BE⊥DG;
(2)证明:如图, 由三角形中位线定理可得:MP∥BE,MP=![]() BE, PN∥DG,PN
BE, PN∥DG,PN![]() =DG,
=DG,
∴PM=PN,∠MPN=∠BOD=90°,
即△MPN是等腰直角三角形;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目