题目内容
如图：在矩形ABDC中，对角线AC和BD交于点O，试说明点A、B、C、D在同一个圆上，并画出这个圆．
解：∵四边形ABDC是矩形，∴AD=BC，OA=OD，OB=OC，
∴OA=OB=OC=OD，
即A、B、C、D在以点O为圆心、OA为半径的圆上．
分析：要说明几点共圆的问题，只需证明这几个点到同一个点的距离相等，此题可以充分运用矩形的性质进行证明．
点评：此题考查了点和圆的位置关系，要掌握证明几点共圆的方法：即证明这些点到同一个点的距离相等．
练习册系列答案
备战中考寒假系列答案
相关题目
14、如图，在矩形ABDC中，E、F分别为AB、CD的中点，现将矩形ACFE沿EF折线折起，则折叠前后线段AF变化情况为（ ）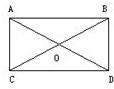
40、如图：在矩形ABDC中，对角线AC和BD交于点O，试说明点A、B、C、D在同一个圆上，并画出这个圆．
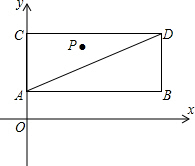边上）的一个动点，点C在y轴上，抛物线y=ax2+bx+1以P为顶点．