Question

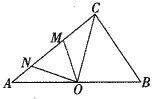
【题目】如图，O为Rt△ABC斜边中点，AB=10，BC=6，M、N在AC边上，若△OMN∽△BOC，点M的对应点是O，则CM=______．

Answer 1

【答案】

【解析】

根据直角三角形斜边中线的性质可得OC=OA=OB=AB，根据等腰三角形的性质可得∠A=∠OCA，∠OCB=∠B，由相似三角形的性质可得∠ONC=∠OCB，，可得OM=MN，利用等量代换可得∠ONC=∠B，即可证明△CNO∽△ABC，利用外角性质可得∠ACO=∠MOC，可得OM=CM，即可证明CM=CN，利用勾股定理可求出AC的长，根据相似三角形的性质即可求出CN的长，即可求出CM的长.

∵O为Rt△ABC斜边中点，AB=10，BC=6，

∴OC=OA=OB=AB=5，AC==8，

∴∠A=∠OCA，∠OCB=∠B，

∵△OMN∽△BOC，

∴∠ONC=∠OCB，，∠COB=∠OMN，

∴MN=OM，∠ONC=∠B，

∴△CNO∽△ABC，

∴，即，

解得：CN=，

∵∠OMN=∠OCM+∠MOC，∠COB=∠A+∠OCA，

∴∠OCM=∠MOC，

∴OM=CM，

∴CM=MN=CN=.

故答案为：