题目内容
【题目】阅读短文,解决问题
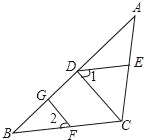
如果一个三角形和一个菱形满足条件:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”.如图1,菱形AEFD为△ABC的“亲密菱形”.
如图2,在△ABC中,以点A为圆心,以任意长为半径作弧,交AB、AC于点M、N,再分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
(1)求证:四边形AEFD是△ABC的“亲密菱形”;
(2)当AB=6,AC=12,∠BAC=45°时,求菱形AEFD的面积.


【答案】(1)证明见解析;(2) 四边形![]() 的面积为
的面积为![]() .
.
【解析】(1)根据尺规作图可知AF平分∠BAC,再根据DF//AC,可得AD=DF,再由两组对边分别平行的四边形是平行四边形可得四边形AEFD是平行四边形,继而可得平行四边形AEFD是菱形,根据“亲密菱形”的定义即可得证;
(2)设菱形的边长为a,即DF=AD=a,则BD=6-a,可证得△BDF∽△BAC,根据相似三角形的性质可求得a=4,过D作DG⊥AC,垂足为G,在Rt△ADG中, DG=2![]() ,继而可求得面积.
,继而可求得面积.
(1)由尺规作图可知AF平分∠BAC,
∴∠DAF=∠EAF,
∵DF//AC,∴∠DFA=∠EAF,∴∠DAF=∠DFA,∴AD=DF,
∵FD//AC,FE//AB,∴四边形AEFD是平行四边形,
∴平行四边形AEFD是菱形,
∵∠BAC与∠DAE重合,点F点BC上,
∴菱形AEFD为△ABC的“亲密菱形”;
(2)设菱形的边长为a,即DF=AD=a,则BD=6-a,
∵DF//AC,∴△BDF∽△BAC,
∴BD:BA=BF:AC,
即(6-a):6=a:12,
∴a=4,
过D作DG⊥AC,垂足为G,
在Rt△ADG中,∠DAG=45°,∴DG=![]() AD=2
AD=2![]() ,
,
∴S菱形AEFD=AEDG=8![]() ,
,
即四边形AEFD的面积为8![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】弹簧挂上物体后会伸长,若一弹簧长度(cm)与所挂物体质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
则下列说法错误的是( )
A.弹簧长度随物体的质量的变化而变化,物体的质量是自变量,弹簧的长度是因变量
B.如果物体的质量为x kg,那么弹簧的长度y cm可以表示为y=12+0.5x
C.在弹簧能承受的范围内,当物体的质量为7kg时,弹簧的长度为16cm
D.在没挂物体时,弹簧的长度为12cm
【题目】甲、乙两名同学在一次用频率估计概率的实验中,统计了某一个结果出现的频率,绘制了如下的表格,则符合这一结果的实验可能是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1200 |
频率 | 0.430 | 0.360 | 0.320 | 0.328 | 0.330 | 0.329 |
A. 抛一枚质地均匀的硬币,出现正面的概率
B. 从一个装有3个红球和2个白球的不透明袋子里任取1球,取出红球的概率
C. 掷一枚均匀的正方体骰子,出现的点数是3的倍数的概率
D. 从正方形、正五边形、正六边形中任意取一个图形,是轴对称图形的概率