题目内容
在Rt△ABC中，∠C=90°，CD⊥AB于点D，若AD=9，BD=4，则AC= ．
考点：相似三角形的判定与性质,射影定理
专题：
分析：根据题意画出图形，先根据相似三角形的判定定理得出△ACD∽△CBD，再由相似三角形的对应边成比例求出CD的长，根据勾股定理即可得出AC的长．
解答：
解：如图所示：
∵Rt△ABC中∠C=90°，CD⊥AB，
∴∠A+∠B=90°，∠A+∠ACD=90°，∠B+∠BCD=90°，
∴∠A=∠BCD，
∴△ACD∽△CBD，
∴
=
，即CD2=AD•BD=9×4=36，解得CD=6，
在Rt△ACD中，
∵AD=9，CD=6，
∴AC=
=
=3
．
故答案为：3
．
解：如图所示：∵Rt△ABC中∠C=90°，CD⊥AB，
∴∠A+∠B=90°，∠A+∠ACD=90°，∠B+∠BCD=90°，
∴∠A=∠BCD，
∴△ACD∽△CBD，
∴
| CD |
| AD |
| BD |
| CD |
在Rt△ACD中，
∵AD=9，CD=6，
∴AC=
| AD2+CD2 |
| 92+62 |
| 13 |
故答案为：3
| 13 |
点评：本题考查的是相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列事件中是必然事件的是（ ）
| A、从一个装有黄、白两色球的缸里摸出一个球，摸出的球是白球 |
| B、小丹的自行车轮胎被钉子扎坏 |
| C、小红期末考试数学成绩一定得满分 |
| D、将豆油滴入水中，豆油会浮在水面上 |
若关于x的方程（x+1）2=k-1没有实数根，则k的取值范围是（ ）
| A、k≤1 | B、k＜1 |
| C、k≥1 | D、k＞1 |
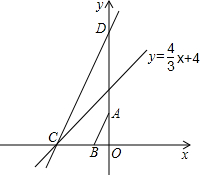如图，在平面直角坐标系中，直线CD交x轴、y轴于点C、D，点B在x轴上，且点B、C到坐标原点O的距离的比为1：3，点D在y轴上，且AD的长为7，若tan∠OCD=3，sin∠ABO=