题目内容
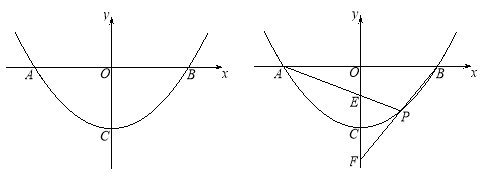
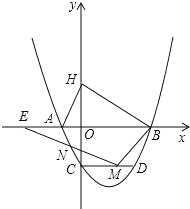
【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(4,0),与y轴交于C(0,﹣2).
(1)求抛物线的解析式;
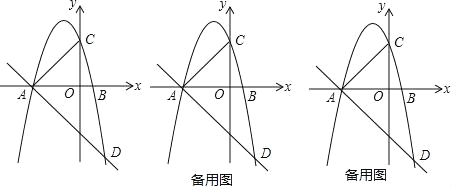
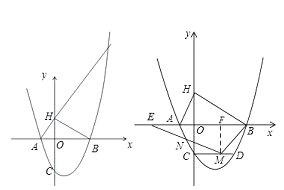
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)P的坐标为(﹣1,0)或(8,18);(3)E的坐标为(﹣
x﹣2;(2)P的坐标为(﹣1,0)或(8,18);(3)E的坐标为(﹣![]() ,0).
,0).
【解析】
试题分析:(1)由抛物线与x轴交于A(﹣1,0),B(4,0),可设抛物线的解析式为y=a(x+1)(x﹣4),然后将(0,﹣2)代入解析式即可求出a的值;(2)当△PBH与△AOC相似时,△PBH是直角三角形,由![]() 可知∠AHB=90°,根据待定系数法求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m=
可知∠AHB=90°,根据待定系数法求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m=![]() 时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.
时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.
试题解析:(1)∵抛物线与x轴交于A(﹣1,0),B(4,0),
∴设抛物线的解析式为:y=a(x+1)(x﹣4),
把(0,﹣2)代入y=a(x+1)(x﹣4),
∴a=![]() ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)当△PBH与△AOC相似时,
∴△AOC是直角三角形,
∴△PBH也是直角三角形,
由题意知:H(0,2),
∴OH=2,
∵A(﹣1,0),B(4,0),
∴OA=1,OB=4,
∴![]()
∵∠AOH=∠BOH,
∴△AOH∽△BOH,
∴∠AHO=∠HBO,
∴∠AHO+∠BHO=∠HBO+∠BHO=90°,
∴∠AHB=90°,
设直线AH的解析式为:y=kx+b,
把A(﹣1,0)和H(0,2)代入y=kx+b,
∴![]() ,
,
∴解得k=2,b=2,
∴直线AH的解析式为:y=2x+2,
联立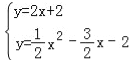 ,
,
解得:x=1或x=﹣8,
当x=﹣1时,
y=0,
当x=8时,
y=18
∴P的坐标为(﹣1,0)或(8,18)
(3)过点M作MF⊥x轴于点F,
设点E的坐标为(n,0),M的坐标为(m,0),
∵∠BME=∠BDC,
∴∠EMC+∠BME=∠BDC+∠MBD,
∴∠EMC=∠MBD,
∵CD∥x轴,
∴D的纵坐标为﹣2,
令y=﹣2代入y=![]() x2﹣
x2﹣![]() x﹣2,
x﹣2,
∴x=0或x=3,
∴D(3,﹣2),
∵B(4,0),
∴由勾股定理可求得:BD=![]() ,
,
∵M(m,0),
∴MD=3﹣m,CM=m(0≤m≤3)
∴由抛物线的对称性可知:∠NCM=∠BDC,
∴△NCM∽△MDB,
∴![]() ,
,
∴![]() ,
,
∴CN=![]() ,
,
∴当m=![]() 时,CN可取得最大值,
时,CN可取得最大值,
∴此时M的坐标为(![]() ,﹣2),
,﹣2),
∴MF=2,BF=![]() ,MD=
,MD=![]()
∴由勾股定理可求得:MB=![]() ,
,
∵E(n,0),
∴EB=4﹣n,
∵CD∥x轴,
∴∠NMC=∠BEM,∠EBM=∠BMD,
∴△EMB∽△BDM,
∴![]() ,
,
∴MB2=MDEB,
∴![]() =
=![]() ×(4﹣n),
×(4﹣n),
∴n=﹣![]() ,
,
∴E的坐标为(﹣![]() ,0).
,0).

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案