题目内容
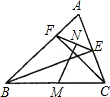 (经典题)如图所示,锐角△ABC中,BE,CF是高,点M,N分别为BC,EF中点.
(经典题)如图所示,锐角△ABC中,BE,CF是高,点M,N分别为BC,EF中点.求证:MN⊥EF.
分析:找到图中直角三角形和斜边上的中线,得到等腰三角形FME,即可解答.
解答: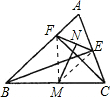 证明:连接ME,MF.
证明:连接ME,MF.
则有ME=
BC,MF=
BC(直角三角形斜边上的中线等于斜边的一半).
∴ME=MF.
又∵N为EF中点,
∴MN⊥EF.
 证明:连接ME,MF.
证明:连接ME,MF.则有ME=
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=MF.
又∵N为EF中点,
∴MN⊥EF.
点评:关键问题是作出MF和ME两条辅助线.

练习册系列答案
相关题目
 63、(经典题)如图所示,完成下列填空.
63、(经典题)如图所示,完成下列填空.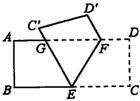 18、(经典题)如图所示,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G,已知∠EFG=58°,求∠BEG度数.
18、(经典题)如图所示,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G,已知∠EFG=58°,求∠BEG度数. 19、(经典题)如图所示,工人师傅在加工零件时,发现AB∥CD,∠A=40°,∠E=80°,小芳用学过的知识,得出∠C=
19、(经典题)如图所示,工人师傅在加工零件时,发现AB∥CD,∠A=40°,∠E=80°,小芳用学过的知识,得出∠C=