题目内容
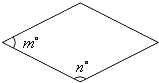
【题目】三种不同类型的纸板的长宽如图所示，其中A类和C类是正方形，B类是长方形，现A类有1块，B类有4块，C类有5块. 如果用这些纸板拼成一个正方形，发现多出其中1块纸板，那么拼成的正方形的边长是（ ）
A. m+n B. 2m+2n C. 2m+n D. m+2n
【答案】D
【解析】
根据题意得到所求的正方形的面积等于一张正方形A类卡片、4张正方形B类卡片和4张长方形C类卡片的和，则所求正方形的面积=m2+4mn +4n2,运用完全平方公式得到所求正方形的面积=（m+2n）2，则所求正方形的边长为m+2n．
解：∵所求的正方形的面积等于一张正方形A类卡片、4张正方形B类卡片和4张长方形C类卡片的和，
∴所求正方形的面积=m2+4mn +4n2=（m+2n）2，
∴所求正方形的边长为m+2n．
故选：D.
练习册系列答案
相关题目
