题目内容
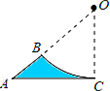
 某工件的形状如图,其中弧BC与AC切于点C,与AB相交于点B,且线段AB的延长线经过弧BC所在圆的圆心.已知AC=4,AB=4
某工件的形状如图,其中弧BC与AC切于点C,与AB相交于点B,且线段AB的延长线经过弧BC所在圆的圆心.已知AC=4,AB=4| 2 |
分析:设圆的半径为r,先根据勾股定理列式求出r=4,从而得到△ABO是等腰直角三角形,然后根据工件的面积等于三角形的面积减去扇形的面积,列式进行计算即可求解.
解答:解:设圆的半径为r,
∵弧BC与AC切于点C,
∴△ACO是直角三角形,
根据勾股定理,AO2=AC2+CO2,
∵AC=4,AB=4
-4,
∴AO=4
-4+r,
∴(4
-4+r)2=42+r2,
整理得,(4
-4)2+2(4
-4)r+r2=16+r2,
即8(
-1)r=32(
-1),
解得r=4,
∴△ACO是等腰直角三角形,
∴∠O=45°,
工件面积=S△ACO-S扇形BOC=
×4×4-
=8-2π.
故选A.
∵弧BC与AC切于点C,
∴△ACO是直角三角形,
根据勾股定理,AO2=AC2+CO2,
∵AC=4,AB=4
| 2 |
∴AO=4
| 2 |
∴(4
| 2 |
整理得,(4
| 2 |
| 2 |
即8(
| 2 |
| 2 |
解得r=4,
∴△ACO是等腰直角三角形,
∴∠O=45°,
工件面积=S△ACO-S扇形BOC=
| 1 |
| 2 |
| 45°•π•42 |
| 360° |
故选A.
点评:本题考查了扇形的面积的计算,勾股定理,切线的性质,判定出△ACO是等腰直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
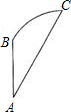 某工件的形状如图所示,圆弧的度数为60°,AB=6cm,点B与点C的距离等于AB,∠BAC=30°,则此工件的面积为
某工件的形状如图所示,圆弧的度数为60°,AB=6cm,点B与点C的距离等于AB,∠BAC=30°,则此工件的面积为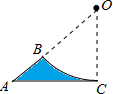 某工件的形状如图,其中弧BC与AC切于点C,与AB相交于点B,且线段AB的延长线经过弧BC所在圆的圆心.已知AC=4,AB=4
某工件的形状如图,其中弧BC与AC切于点C,与AB相交于点B,且线段AB的延长线经过弧BC所在圆的圆心.已知AC=4,AB=4 -4,则工件的面积是
-4,则工件的面积是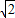 -4,则工件的面积是( )
-4,则工件的面积是( )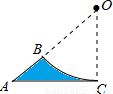
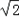 ﹣4,则工件的面积是
﹣4,则工件的面积是