题目内容
（2011•攀枝花）一个不透明的袋子中，装有红黑两种颜色的小球（除颜色不同外其他都相同），其中一个红球，两个分别标有A、B黑球．
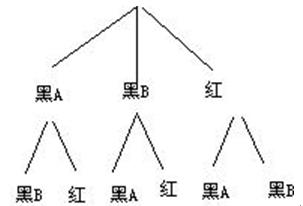
（1）小李第一次从口袋中摸出一个球，并且不放回，第二次又从口袋中摸出一个球，则小李两次都摸出黑球的概率是多少？试用树状图或列表法加以说明；
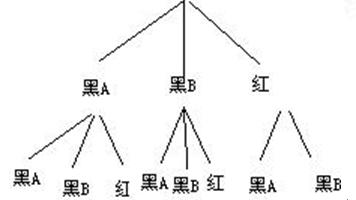
（2）小张第一次从口袋中摸出一个球，摸到红球不放回，摸到黑球放回．第二次又从口袋中摸出一个球，则小张第二次摸到黑球的概率是多少？试用
树状图或列表法加以说明．
解：（1）共6种情况，两次都摸出黑球的情况数有2种，所以概率为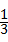
；
（2）共8种情况，第2次摸出黑球的情况数有6种，所以概率为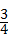
．
解析
练习册系列答案
相关题目
+（1﹣π）0+
．
（2011•攀枝花）下列各命题中，真命题是（ ）
| A．对角线相等且互相垂直的四边形是正方形 | |
| B．如果两个三角形有两条边和一个角分别对应相等，那么这两个三角形一定全等 | |
| C．角平分线上任意一点到这个角的两边的距离相等 | D．相等的圆周角所对的弧相等 |
（2011•攀枝花）要使
有意义，则x应该满足（ ）
有意义，则x应该满足（ ）| A．0≤x≤3 | B．0＜x≤3且x≠1 |
| C．1＜x≤3 | D．0≤x≤3且x≠1 |
