题目内容
探索与发现,△ABC中,AD是BC边上的高,AE是∠BAC的平分线.
(1)如图,若∠B=20°,∠C=58°,求∠EAD的度数.

(2)如图,当∠B和∠C(∠C>∠B)为锐角时,由第1小题的计算过程,猜想∠EAD、∠B和∠C之间的关系是______(不必说明理由).
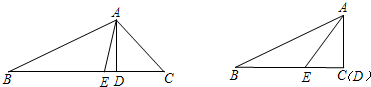
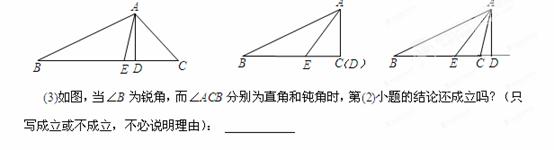
(3)如图,当∠B为锐角,而∠ACB分别为直角和钝角时,第(2)小题的结论还成立吗?(只写成立或不成立,不必说明理由):______

解:(1)∵∠B=20°,∠C=58°,
∴∠BAC=180°-∠B-∠C=102°,
而AE是∠BAC的平分线,
∴∠EAC= ∠BAC=51°,
∠BAC=51°,
又∵AD是BC边上的高,
∴∠DAC=90°-∠C=32°,
∴∠EAD=∠EAC-∠DAC=51°-32°=19°;
(2)∠EAD= (∠C-∠B);
(∠C-∠B);
(3)成立.
分析:(1)先根据三角形的内角和定理求得∠BAC=180°-∠B-∠C=102°,利用角平分线的定义得∠EAC= ∠BAC=51°,而∠DAC=90°-∠C=32°,通过∠EAD=∠EAC-∠DAC即可得到结果.
∠BAC=51°,而∠DAC=90°-∠C=32°,通过∠EAD=∠EAC-∠DAC即可得到结果.
(2)和(1)一样:∠EAC=90°- ∠B-
∠B- ∠C,而∠DAC=90°-∠C,则可得∠EAD=∠EAC-∠DAC=
∠C,而∠DAC=90°-∠C,则可得∠EAD=∠EAC-∠DAC= (∠C-∠B);
(∠C-∠B);
(3)∠B为锐角,而∠ACB分别为直角和钝角时,证明的方法一样.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的角平分线和高的性质.
∴∠BAC=180°-∠B-∠C=102°,
而AE是∠BAC的平分线,
∴∠EAC=
 ∠BAC=51°,
∠BAC=51°,又∵AD是BC边上的高,
∴∠DAC=90°-∠C=32°,
∴∠EAD=∠EAC-∠DAC=51°-32°=19°;
(2)∠EAD=
 (∠C-∠B);
(∠C-∠B);(3)成立.
分析:(1)先根据三角形的内角和定理求得∠BAC=180°-∠B-∠C=102°,利用角平分线的定义得∠EAC=
 ∠BAC=51°,而∠DAC=90°-∠C=32°,通过∠EAD=∠EAC-∠DAC即可得到结果.
∠BAC=51°,而∠DAC=90°-∠C=32°,通过∠EAD=∠EAC-∠DAC即可得到结果.(2)和(1)一样:∠EAC=90°-
 ∠B-
∠B- ∠C,而∠DAC=90°-∠C,则可得∠EAD=∠EAC-∠DAC=
∠C,而∠DAC=90°-∠C,则可得∠EAD=∠EAC-∠DAC= (∠C-∠B);
(∠C-∠B);(3)∠B为锐角,而∠ACB分别为直角和钝角时,证明的方法一样.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的角平分线和高的性质.

练习册系列答案
相关题目

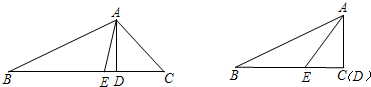
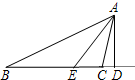
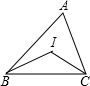 实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,
实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,