Question

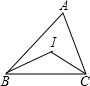实践与探索！如图，△ABC中，∠ABC与∠ACB的平分线交于点I，根据下列条件，求∠BIC的度数，
①若∠ABC=40°，∠ACB=60°，则∠BIC=

 

；
②若∠ABC+∠ACB=80°，则∠BIC=

 

；
③若∠A=120°，则∠BIC=

 

；
④从上述计算中，我们能发现∠BIC与∠A的关系式，并加以证明．

Answer 1

分析：①由∠ABC=40°，∠ACB=60°，∠ABC与∠ACB的平分线交于点I，可求∠IBC、∠ICB的度数，再利用三角形内角和定理求∠BIC；
②由∠ABC+∠ACB=80°，∠ABC与∠ACB的平分线交于点I，可求∠IBC+∠ICB的度数，再利用三角形内角和定理求∠BIC；
③由∠A=120°可知∠ABC+∠ACB=60°，∠ABC与∠ACB的平分线交于点I，可求∠IBC+∠ICB的度数，再利用三角形内角和定理求∠BIC；
④由三角形内角和定理得∠ABC+∠ACB=180°-∠A，∠ABC与∠ACB的平分线交于点I，则∠IBC+∠ICB=

1

2

∠ABC+

1

2

∠ACB=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A），在△IBC中，利用三角形内角和定理求∠BIC．

解答：解：①∵∠ABC=40°，∠ACB=60°，∠ABC与∠ACB的平分线交于点I，
∴∠IBC=20°∠ICB=30°，
∴∠BIC=180°-∠IBC-∠ICB=130°；
②∵∠ABC+∠ACB=80°，∠ABC与∠ACB的平分线交于点I，
∴∠IBC+∠ICB=

1

2

（∠ABC+∠ACB）=40°，
∴∠BIC=180°-（∠IBC+∠ICB）=140°；
③∵∠A=120°，
∴∠ABC+∠ACB=60°，
又∵∠ABC与∠ACB的平分线交于点I，
∴∠IBC+∠ICB=

1

2

（∠ABC+∠ACB）=30°，
∴∠BIC=180°-（∠IBC+∠ICB）=150°；
④∠BIC=90°+

1

2

∠A
理由如下：在△ABC中，∠ABC+∠ACB=180°-∠A
∵BI、CI是△ABC内角的平分线
∴∠IBC=

1

2

∠ABC，∠ICB=

1

2

∠ACB
∴∠IBC+∠ICB=

1

2

∠ABC+

1

2

∠ACB=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A）
在△IBC中，
∠BIC=180°-（∠IBC+∠ICB）=180°-

1

2

（180°-∠A）=90°+

1

2

∠A
即：∠BIC=90°+

1

2

∠A．

点评：本题考查了三角形角平分线的性质，内角和定理的运用．