题目内容
如图所示，五边形ABCDE中，AB=AE，BC=DE，∠ABC=∠AED，点F是CD的中点．求证：AF⊥CD．
分析：连接AC，AD，可证明△ABC≌△AED，进而得到AC=AD，再利用等腰三角形的性质：三线合一即可得到AF⊥CD．
解答：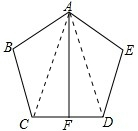
证明：连接AC，AD，
在△ABC和△AED中，
，
∴△ABC≌△AED（SAS），
∴AC=AD，
∵点F是CD的中点，
∴AF⊥CD．
证明：连接AC，AD，在△ABC和△AED中，
|
∴△ABC≌△AED（SAS），
∴AC=AD，
∵点F是CD的中点，
∴AF⊥CD．
点评：本题考查了全等三角形的判定和性质以及等腰三角形的判定和性质，解题的关键是连接AC，AD构造全等三角形．
练习册系列答案
相关题目
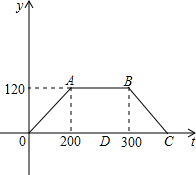小明参加汽车驾驶培训，在实际操作考试时，被要求进行启动加速、匀速运行、制动减速三个连贯过程，在加速和减速运动过程中，路程和速度均满足关系s=
，
，
，
，
…的圆心依次接A、B、C、D、E循环，它们依次相连接，如果AB＝1，那么曲线EFGHIJ的长度为________(结果保留π)．