题目内容
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)点D是抛物线上的一动点,是否存在点D,使得tan∠DCB=tan∠ACO.若存在,请求出点D的坐标,若不存在,说明理由.

【答案】(1)y=﹣2x2+x+3;(2)∠ACB=45°;(3)D点坐标为(1,2)或(4,﹣25).
【解析】
(1)设交点式y=a(x+1)(x﹣![]() ),展开得到﹣
),展开得到﹣![]() a=3,然后求出a即可得到抛物线解析式;
a=3,然后求出a即可得到抛物线解析式;
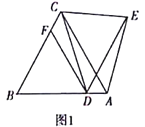
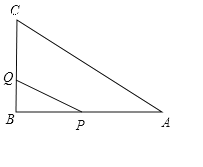
(2)作AE⊥BC于E,如图1,先确定C(0,3),再分别计算出AC=![]() ,BC=
,BC=![]() ,接着利用面积法计算出AE=
,接着利用面积法计算出AE=![]() ,然后根据三角函数的定义求出∠ACE即可;
,然后根据三角函数的定义求出∠ACE即可;
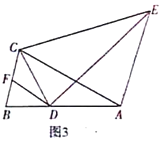
(3)作BH⊥CD于H,如图2,设H(m,n),证明Rt△BCH∽Rt△ACO,利用相似计算出BH=![]() ,CH=
,CH=![]() ,再根据两点间的距离公式得到(m﹣
,再根据两点间的距离公式得到(m﹣![]() )2+n2=(
)2+n2=(![]() )2,m2+(n﹣3)2=(
)2,m2+(n﹣3)2=(![]() )2,接着通过解方程组得到H(
)2,接着通过解方程组得到H(![]() ,﹣
,﹣![]() )或(
)或(![]() ),然后求出直线CD的解析式,与二次函数联立成方程组,解方程组即可.
),然后求出直线CD的解析式,与二次函数联立成方程组,解方程组即可.
(1)设抛物线解析式为y=a(x+1)(x﹣![]() ),即y=ax2﹣
),即y=ax2﹣![]() ax﹣
ax﹣![]() a,∴﹣
a,∴﹣![]() a=3,解得:a=﹣2,∴抛物线解析式为y=﹣2x2+x+3;
a=3,解得:a=﹣2,∴抛物线解析式为y=﹣2x2+x+3;
(2)作AE⊥BC于E,如图1,当x=0时,y=﹣2x2+x+3=3,则C(0,3),而A(﹣1,0),B(![]() ,0),∴AC=
,0),∴AC=![]() =
=![]() ,BC=
,BC=![]() =
=![]()
![]() AEBC=
AEBC=![]() OCAB,∴AE=
OCAB,∴AE=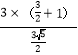 =
=![]() .
.
在Rt△ACE中,sin∠ACE=![]() =
=![]() =
=![]() ,∴∠ACE=45°,即∠ACB=45°;
,∴∠ACE=45°,即∠ACB=45°;
(3)作BH⊥CD于H,如图2,设H(m,n).
∵tan∠DCB=tan∠ACO,∴∠HCB=∠ACO,∴Rt△BCH∽Rt△ACO,∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,∴BH=
,∴BH=![]() ,CH=
,CH=![]() ,∴(m﹣
,∴(m﹣![]() )2+n2=(
)2+n2=(![]() )2=
)2=![]() ,①
,①
m2+(n﹣3)2=(![]() )2=
)2=![]() ,②
,②
②﹣①得m=2n+![]() ,③,把③代入①得:(2n+
,③,把③代入①得:(2n+![]() ﹣
﹣![]() )2+n2=
)2+n2=![]() ,整理得:80n2﹣48n﹣9=0,解得:n1=﹣
,整理得:80n2﹣48n﹣9=0,解得:n1=﹣![]() ,n2=
,n2=![]() .
.
当n=﹣![]() 时,m=2n+
时,m=2n+![]() =
=![]() ,此时H(
,此时H(![]() ,﹣
,﹣![]() ),易得直线CD的解析式为y=﹣7x+3,解方程组
),易得直线CD的解析式为y=﹣7x+3,解方程组![]() 得:
得:![]() 或
或![]() ,此时D点坐标为(4,﹣25);
,此时D点坐标为(4,﹣25);
当n=![]() 时,m=2n+
时,m=2n+![]() =
=![]() ,此时H(
,此时H(![]() ),易得直线CD的解析式为y=﹣x+3,解方程组
),易得直线CD的解析式为y=﹣x+3,解方程组![]() 得:
得:![]() 或
或![]() ,此时D点坐标为(1,2).
,此时D点坐标为(1,2).
综上所述:D点坐标为(1,2)或(4,﹣25).

 永乾教育寒假作业快乐假期延边人民出版社系列答案
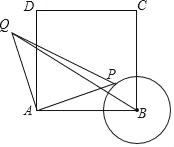
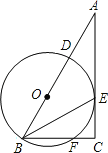
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
【题目】甲、乙两名同学的家与学校的距离均为![]() .甲同学先步行
.甲同学先步行![]() ,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的
,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的![]() 倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到
倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到![]() .
.
(1)解:设乙同学骑自行车的速度为![]() .完成表格:
.完成表格:
乙同学 | 甲同学 | ||
骑自行车 | 步行 | 乘公交车 | |
路程 |
|
| |
时间 |
| ||
(2)求乙同学骑自行车的速度.
(3)当甲同学到达学校时,乙同学离学校还有多少米?
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)
【题目】今年春北方严重干旱,某社区人畜饮水紧张,每天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨,从两水厂运水到社区供水点的路程和运费如下表:
到社区供水点的路程(千米) | 运费(元/吨·千米) | |
甲厂 | 20 | 12 |
乙厂 | 14 | 15 |
【1】若某天调运水的总运费为26700元,则从甲、乙两水厂各调运多少吨饮用水?
【2】设从甲厂调运饮用水![]() 吨,总运费为W元,试写出W关于与
吨,总运费为W元,试写出W关于与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?