题目内容
如图1,直线y=x与直线y=-2x+4交于点A,点P是直线OA上一动点,作PQ∥x轴交直线y=-2x+4于点Q,以PQ为边,向下作正方形PQMN,设点P的横坐标为t.
(1)求交点A的坐标;
(2)求点P从点O运动到点A过程中,正方形PQMN与△OAB重叠的面积S与t的函数关系式;
(3)是否存在点Q,使△OCQ为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)求交点A的坐标;
(2)求点P从点O运动到点A过程中,正方形PQMN与△OAB重叠的面积S与t的函数关系式;
(3)是否存在点Q,使△OCQ为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

分析: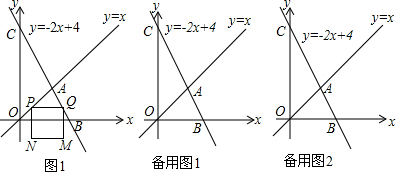 (1)由题意可联立得方程组
(1)由题意可联立得方程组
,解此方程组即可求得交点A的坐标;
(2)由P(t,t),PQ∥x轴交直线y=-2x+4于点Q,可得Q(
,t),然后由当点N落在x轴上时,PN=PQ,求得t的值,然后分别从当0<t≤
时与当
<t≤
时去分析求解即可求得答案;
(3)首先求得点B与C的坐标,继而求得BC的长,再分别从若CQ1=OQ1,若OC=CQ=4与若OQ4=OC=4时去分析求解即可求得答案.
 (1)由题意可联立得方程组
(1)由题意可联立得方程组
|
(2)由P(t,t),PQ∥x轴交直线y=-2x+4于点Q,可得Q(
| 4-t |
| 2 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
(3)首先求得点B与C的坐标,继而求得BC的长,再分别从若CQ1=OQ1,若OC=CQ=4与若OQ4=OC=4时去分析求解即可求得答案.
解答:解:(1)联立得方程组
,
解得:
,
故交点A的坐标为A(
,
);
(2)∵P(t,t),PQ∥x轴交直线y=-2x+4于点Q,
∴Q(
,t),
∴PQ=
-t=
,
当点N落在x轴上时,
∵PN=PQ
∴t=
,
解得:t=
,
①当0<t≤
时,S=t•
=-
t2+2t;
②当
<t≤
时,S=PQ2=(
)2=
t2-6t+4;
(3)存在点Q,使△OCQ为等腰三角形.
∵点C是直线y=-2x+4与y轴的交点,与x轴交于点B,
∴点C(0,4),B(2,0),
即OC=4,OB=2,
∴BC=
=2
,
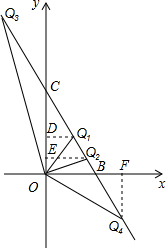 ①若CQ1=OQ1,过点Q1作Q1D⊥OC,
①若CQ1=OQ1,过点Q1作Q1D⊥OC,
则OD=
OC=2,
当y=2时,即-2x+4=2,
解得:x=1,
∴点Q1(1,2);
②若OC=CQ=4,
过点Q2作Q2E⊥OC于点E,则Q2E∥OB,
∴△CQ2E∽△CBO,
∴
=
,
即
=
,
解得:Q2E=
,
∴当x=
时,y=-2×
+4=4-
,
∴点Q2(
,4-
);
同理:点Q3(-
,4+
);
③若OQ4=OC=4时,过点Q4作Q4F⊥x轴,
设点Q4(x,-2x+4),
∴x2+(-2x+4)2=16,
解得:x=
,x=0(舍去),
∴点Q4(
,-
);
综上可得:一共有4个点满足,分别为:Q1(1,2),Q2(
,4-
),Q3(-
,4+
),Q4(
,-
).
|
解得:
|
故交点A的坐标为A(
| 4 |
| 3 |
| 4 |
| 3 |
(2)∵P(t,t),PQ∥x轴交直线y=-2x+4于点Q,
∴Q(
| 4-t |
| 2 |
∴PQ=
| 4-t |
| 2 |
| 4-3t |
| 2 |
当点N落在x轴上时,
∵PN=PQ
∴t=
| 4-3t |
| 2 |
解得:t=
| 4 |
| 5 |
①当0<t≤
| 4 |
| 5 |
| 4-3t |
| 2 |
| 3 |
| 2 |
②当
| 4 |
| 5 |
| 4 |
| 3 |
| 4-3t |
| 2 |
| 9 |
| 4 |
(3)存在点Q,使△OCQ为等腰三角形.
∵点C是直线y=-2x+4与y轴的交点,与x轴交于点B,
∴点C(0,4),B(2,0),
即OC=4,OB=2,
∴BC=
| OC2+OB2 |
| 5 |
 ①若CQ1=OQ1,过点Q1作Q1D⊥OC,
①若CQ1=OQ1,过点Q1作Q1D⊥OC,则OD=
| 1 |
| 2 |
当y=2时,即-2x+4=2,
解得:x=1,
∴点Q1(1,2);
②若OC=CQ=4,
过点Q2作Q2E⊥OC于点E,则Q2E∥OB,
∴△CQ2E∽△CBO,
∴
| Q2E |
| OB |
| CQ2 |
| BC |
即
| Q2E |
| 2 |
| 4 | ||
2
|
解得:Q2E=
4
| ||
| 5 |
∴当x=
4
| ||
| 5 |
4
| ||
| 5 |
8
| ||
| 5 |
∴点Q2(
4
| ||
| 5 |
8
| ||
| 5 |
同理:点Q3(-
4
| ||
| 5 |
8
| ||
| 5 |
③若OQ4=OC=4时,过点Q4作Q4F⊥x轴,
设点Q4(x,-2x+4),
∴x2+(-2x+4)2=16,
解得:x=
| 16 |
| 5 |
∴点Q4(
| 16 |
| 5 |
| 12 |
| 5 |
综上可得:一共有4个点满足,分别为:Q1(1,2),Q2(
4
| ||
| 5 |
8
| ||
| 5 |
4
| ||
| 5 |
8
| ||
| 5 |
| 16 |
| 5 |
| 12 |
| 5 |
点评:此题考查了一次函数的性质、正方形的性质、相似三角形的判定与性质以及等腰三角形的性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
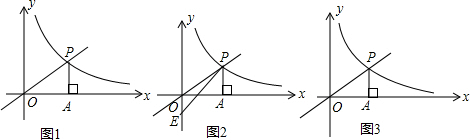

 (k>0,x>0)交于点P,PA⊥x轴于A,S△PAO=
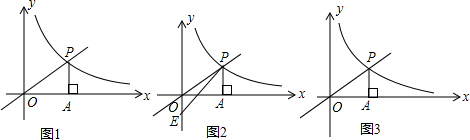
(k>0,x>0)交于点P,PA⊥x轴于A,S△PAO= .
.
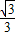 x+
x+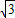 与两坐标轴交于A、B,以点M(1,0)为圆心,MO为半径作小⊙M,又以点M为圆心、MA为半径作大⊙M交坐标轴于C、D.
与两坐标轴交于A、B,以点M(1,0)为圆心,MO为半径作小⊙M,又以点M为圆心、MA为半径作大⊙M交坐标轴于C、D.