题目内容
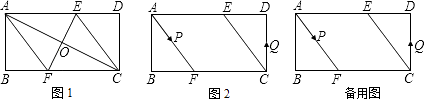
【题目】如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE相交于点O.
(1)求证:四边形ADCE是矩形.
(2)若∠AOE=60°,AE=4,求矩形ADCE对角线的长.

【答案】(1)证明见解析;(2)8.
【解析】分析:(1)根据四边形ABDE是平行四边形和AB=AC,推出AD和DE相等且互相平分,即可推出四边形ADCE是矩形.
(2)根据∠AOE=60°和矩形的对角线相等且互相平分,得出△AOE为等边三角形,即可求出AO的长,从而得到矩形ADCE对角线的长.
详解:(1)∵四边形ABDE是平行四边形,
∴AB=DE,
又∵AB=AC,
∴DE=AC.
∵AB=AC,D为BC中点,
∴∠ADC=90°,
又∵D为BC中点,
∴CD=BD.
∴CD∥AE,CD=AE.
∴四边形AECD是平行四边形,
又∴∠ADC=90°,
∴四边形ADCE是矩形.
(2)∵四边形ADCE是矩形,
∴AO=EO,
∴△AOE为等边三角形,
∴AO=4,
故AC=8.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某电动车厂平均每天计划生产200辆电动车,由于各种原因实际每天的生产量与计划量相比有出入.下表是某周的生产情况(超产为正,减产为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减情况 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(1)产量最多的一天比产量最少的一天多生产多少辆?
(2)根据记录可知前五天共生产多少辆?
(3)该厂实行计件工资制,每辆车100元,超额完成则超额部分每辆车再奖励40元(以一周为单位结算),那么该厂工人这一周的工资总额是多少元?