��Ŀ����
����Ŀ��һ���߲˹�˾�չ�ij����ɫ�߲�140�֣����ӹ���������ۣ����ۺ������������±���ʾ:

��֪�ù�˾�ļӹ������ǣ��ּӹ�ÿ��ӹ������߲˵������Ǿ��ӹ���3���������ּӹ�����ͬʱ���У��ܼ��ڵ����������ƣ���˾������һ��ʱ���ڽ������߲�ȫ���ӹ������ۣ�
��1����Ҫ��15��պüӹ���140���߲ˣ������ɫ�߲��Ⱦ��ӹ�20�֣�ʣ�µ��ٽ��дּӹ������ð�ʱ��ɣ��ӹ��ʹּӹ�ÿ����ܼӹ��Ķ�����
��2����Ҫ��140���߲�ȫ���ӹ��겻����13�죬�������ּӹ���ʽ��Ҫ�У��Ⱦ��ӹ���ּӹ�������������ӹ�ʱ�䣨ʱ��ȡ�������������������Ƕ��٣�
���𰸡���1��ÿ�쾫�ӹ�4�֣���ÿ��ּӹ�12�֣�
��2������2����о��ӹ���11��ּӹ��ɻ��������Ϊ148000Ԫ��
�������������������1�����������ϵΪ�����ӹ�����+�ּӹ�����=15�������г�������⼴�ɣ���2������������ӹ���������ȡֵ��Χ��Ȼ���ʾW�����W���ֵ��
�������: ��1����ÿ�쾫�ӹ�x�֣���ÿ��ּӹ�3 x�֣�������ã�
![]() +
+![]() = 15
= 15
��ã�x=4��
������ã�x=4��ԭ���̵ĸ���
��3x=12��
��ÿ�쾫�ӹ�4�֣���ÿ��ּӹ�12�֣�
��2���辫�ӹ���ʱ��Ϊm�죬�������
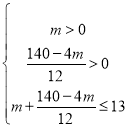
���: ![]()
��ӹ������߲˿ɻ���WԪ����
W=20004m+1000=140000+4000m��Ԫ����0��m��2����
��һ�κ�������֪��W��m���������������
�ʵ�m=2ʱ��Wȡ�����ֵΪ140000+4000��2=148000��Ԫ����
�𣺰���2����о��ӹ���11��ּӹ��ɻ��������Ϊ148000Ԫ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�