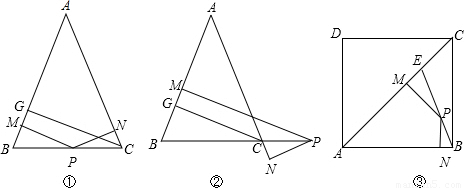
题目内容
如图①,已知△ABC中,AB=AC,点P是BC上的一点,PN⊥AC于点N,PM⊥AB于点M,CG⊥AB于点G,则CG=PM+PN.(1)如图②,若点P在BC的延长线上,则PM、PN、CG三者是否还有上述关系,若有,请说明理由,若没有,猜想三者之间又有怎样的关系,并证明你的猜想;
(2)如图③,AC是正方形ABCD的对角线,AE=AB,点P是BE上任一点,PN⊥AB于点N,PM⊥AC于点M,猜想PM、PN、AC有什么关系;(直接写出结论)
(3)观察图①、②、③的特性,请你根据这一特性构造一个图形,使它仍然具有PM、PN、CG这样的线段,并满足图①或图②的结论,写出相关题设的条件和结论
 .
.
【答案】分析:(1)猜想CG=PM-PN.过C点作CE⊥PM于E,则根据已知条件容易证明四边形CGME是矩形,然后根据矩形的性质可以得到
∠ECP=∠PCN,而∠PNC=∠PEC=90°,PC公共,可以证明△PNC≌△PEC,再根据全等三角形的性质就可以证明猜想的结论;
(2)PM+PN= AC.连接BD,交AC于O,过点P作PF⊥BD于F,由于AE=AB,根据(1)可以得到PM+PN=BO=
AC.连接BD,交AC于O,过点P作PF⊥BD于F,由于AE=AB,根据(1)可以得到PM+PN=BO= BD=
BD= AC;
AC;
(3)点P是等腰三角形底边所在直线上的任意一点,点P到两腰的距离的和(或差)等于这个等腰三角形腰上的高.如图③,④都有BG=PM+PN.如图⑤CG=PM-PN.证明过程也是利用(1)的结论得到CG=PM-PN.
解答: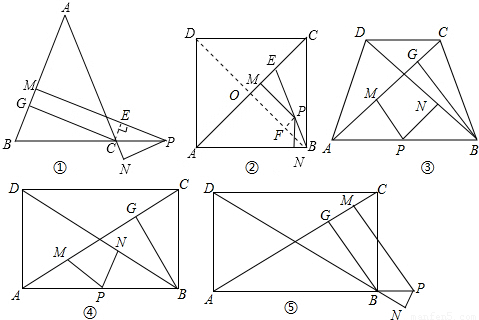
(1)猜想CG=PM-PN
证明:过C点作CE⊥PM于E
∵PN⊥AB,CG⊥AB
∴四边形CGME是矩形
∴ME=CG,CE∥AB
∴∠B=∠ECP
∵AB=AC
∴∠B=∠ACB=∠PCN
∴∠ECP=∠PCN
∵∠PNC=∠PEC=90°,PC=PC
∴△PNC≌△PEC
∴PN=PE
∴CG=ME=PM-PE=PM-PN.(4分)
(2)PM+PN= AC
AC
证明:连接BD,交AC于O,过点P作PF⊥BD于F
∵四边形ABCD是正方形
∴∠COB=90°,OB=OC= AC
AC
∵PM⊥AC
∴四边形PFOM为矩形
∴MP=OF,PF∥AC
∴∠OEP=∠FPB
∵AE=AB
∴∠OEP=∠ABP
∴∠ABP=∠FPB
∵PB=PB,∠PFB=∠PNB=90°
∴△PFB≌△BNP
∴BF=PN
∴OB=OF+FB=PM+PN= AC.(8分)
AC.(8分)
(3)点P是等腰三角形底边所在直线上的任意一点,点P到两腰的距离的和(或差)等于这个等腰三角形腰上的高.
如图③,④都有BG=PM+PN,如图⑤CG=PM-PN.(10分)
点评:此题主要考查了等腰三角形的一个结论:点P是等腰三角形底边所在直线上的任意一点,点P到两腰的距离的和(或差)等于这个等腰三角形腰上的高,然后把这个结论放在不同的图形背景中,进行图形变换,无论变换成什么图形,但结论还是一样.
∠ECP=∠PCN,而∠PNC=∠PEC=90°,PC公共,可以证明△PNC≌△PEC,再根据全等三角形的性质就可以证明猜想的结论;
(2)PM+PN=
 AC.连接BD,交AC于O,过点P作PF⊥BD于F,由于AE=AB,根据(1)可以得到PM+PN=BO=
AC.连接BD,交AC于O,过点P作PF⊥BD于F,由于AE=AB,根据(1)可以得到PM+PN=BO= BD=
BD= AC;
AC;(3)点P是等腰三角形底边所在直线上的任意一点,点P到两腰的距离的和(或差)等于这个等腰三角形腰上的高.如图③,④都有BG=PM+PN.如图⑤CG=PM-PN.证明过程也是利用(1)的结论得到CG=PM-PN.
解答:

(1)猜想CG=PM-PN
证明:过C点作CE⊥PM于E
∵PN⊥AB,CG⊥AB
∴四边形CGME是矩形
∴ME=CG,CE∥AB
∴∠B=∠ECP
∵AB=AC
∴∠B=∠ACB=∠PCN
∴∠ECP=∠PCN
∵∠PNC=∠PEC=90°,PC=PC
∴△PNC≌△PEC
∴PN=PE
∴CG=ME=PM-PE=PM-PN.(4分)
(2)PM+PN=
 AC
AC证明:连接BD,交AC于O,过点P作PF⊥BD于F
∵四边形ABCD是正方形
∴∠COB=90°,OB=OC=
 AC
AC∵PM⊥AC
∴四边形PFOM为矩形
∴MP=OF,PF∥AC
∴∠OEP=∠FPB
∵AE=AB
∴∠OEP=∠ABP
∴∠ABP=∠FPB
∵PB=PB,∠PFB=∠PNB=90°
∴△PFB≌△BNP
∴BF=PN
∴OB=OF+FB=PM+PN=
 AC.(8分)
AC.(8分)(3)点P是等腰三角形底边所在直线上的任意一点,点P到两腰的距离的和(或差)等于这个等腰三角形腰上的高.
如图③,④都有BG=PM+PN,如图⑤CG=PM-PN.(10分)
点评:此题主要考查了等腰三角形的一个结论:点P是等腰三角形底边所在直线上的任意一点,点P到两腰的距离的和(或差)等于这个等腰三角形腰上的高,然后把这个结论放在不同的图形背景中,进行图形变换,无论变换成什么图形,但结论还是一样.

练习册系列答案
相关题目
 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.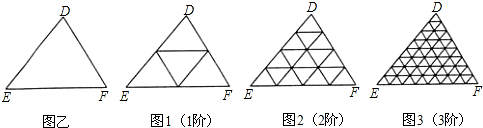
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=

