��Ŀ����
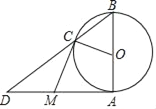
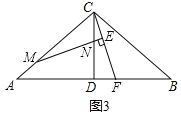
����Ŀ����ͼ����֪��ABC�У�CA=CB��CD��AB��D�㣬��MΪ�߶�AC��һ���㣬�߶�MN��DC�ڵ�N���ҡ�BAC=2��CMN������C��CE��MN��MN�ӳ����ڵ�E�����߶�AB�ڵ�F��̽��![]() ��ֵ.
��ֵ.
��1������ACB=90�㣬��M���A�غϣ���ͼ1��ʱ�����߶�CE��EF֮���������ϵ�� ����![]() = ��
= ��
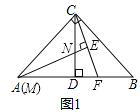
��2���ڣ�1���������£�����M�����A�غϣ���ͼ2���������д��![]() ��ֵ����֤����IJ���
��ֵ����֤����IJ���
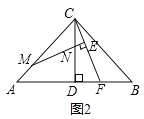
��3������ACB��90�㣬��CAB=![]() �������������䣬��ֱ��д��
�������������䣬��ֱ��д��![]() ��ֵ���ú���
��ֵ���ú���![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
���𰸡���1����CE=EF���� ![]() ����2��
����2��![]() =
=![]() �����ɼ���������3��
�����ɼ���������3��![]() =
=![]() .
.
��������(1)�����ݵ��������ε����ߺ�һ�����ó���EΪCF���е㣬�Ӷ��ó��𰸣�(2)������M��MQ//AB��CD�ڵ�P����CF�ڵ�Q�����ݵ��������Ρ�ֱ�������ε����ʵó���MPN����CPQȫ�ȣ��Ӷ��ó�CE=EQ ��MC=MQ����CE=![]() CQ=
CQ=![]() MN��(3)����ͼ3��ͬ(1)��(2)�ɵ�CE=
MN��(3)����ͼ3��ͬ(1)��(2)�ɵ�CE= ![]() CQ����֤��MPN~��CPQ������
CQ����֤��MPN~��CPQ������![]() ����
����![]() ��
��
(1)����CE=EF���� ![]() ��
��
(2)��![]() =
=![]()
�������£���ͼ2��ʾ������M��MQ//AB��CD�ڵ�P����CF�ڵ�Q��
���С�CMP=��BAC=45�㣬 ��CP=MP��
�ߡ�BAC=2��CMN�� ���CMP=2��CMN�� ���CMN=��NMP=22.5�㣬��CE��MN��
���CEM=��QEM=90�㣬��CE=EQ �����ߺ�һ������CD��AB�� MQ//AB��
��CD��MQ�����MPN=��CPQ=90�㣬�֡ߡ�NCE+��CNE=��NCE+��CQN=90�㣬
���CQN=��CNE=��MNP����CP=MP�����MPN![]() ��CPQ����CE=EQ ��MC=MQ��
��CPQ����CE=EQ ��MC=MQ��
��CE=![]() CQ=
CQ=![]() MN����
MN����![]() =
=![]() ��
��
(3)��![]() =
=![]() ��
��
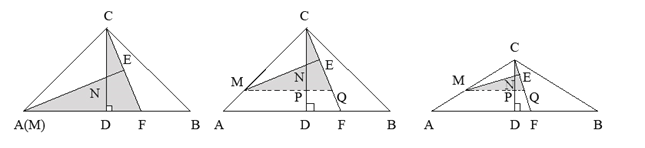
ͼ1 ͼ2 ͼ3

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���Ķ����в��ϣ�
ʵ��������ʾ��һ����˺�250�����ͶȰƺ���ѪҺ�оƾ�����(����/�ٺ���)��ʱ������������ߴﵽ��ֵ��֮��ѪҺ�оƾ�������ʱ����������ͣ�
С������������ݺ�ѧϰ�����ľ��飬��ѪҺ�оƾ�������ʱ��仯�Ĺ��ɽ�����̽��������ѪҺ�оƾ�����y��ʱ��x�ĺ���������y��ʾѪҺ�оƾ�����(����/�ٺ���)��x��ʾ���ƺ��ʱ��(Сʱ)��
�±���¼��6Сʱ��11��ʱ���ѪҺ�оƾ�����y(����/�ٺ���)�����ƺ��ʱ��x(Сʱ)(x��0)�ı仯�����
���ƺ��ʱ��x(Сʱ) | �� |
|
|
| 1 |
|
| 2 | 3 | 4 | 5 | 6 | �� |
ѪҺ�оƾ�����y (����/�ٺ���) | �� |
| 150 |
| 200 |
| 150 |
|
|
| 45 |
| �� |
������С����̽�����̣��벹��������
(1)��ͼ����ƽ��ֱ������ϵxOy�У����ϱ��и�����ֵΪ������㣬ͼ���Ѹ������ֵ㣬�������ʣ��ĵ㣬����ѪҺ�оƾ�����y��ʱ��x�仯�ĺ���ͼ��
(2)�۲�������ݼ�ͼ��ɷ��ִ˺���ͼ����ֱ��x��![]() ��������ò�ͬ�ĺ�������ʽ��ʾ��������ѡ����һ����д������ʽ��
��������ò�ͬ�ĺ�������ʽ��ʾ��������ѡ����һ����д������ʽ��
(3)�����ҹ涨��������ʻ��ԱѪҺ�еľƾ��������ڻ����20����/�ٺ���ʱ���ڡ��ƺ��ʻ�������ܼݳ���·������������ѧģ�ͣ�����ij��ʻԱ����20��00�ڼҺ���250�����ͶȰƣ��ڶ�������6��30�ܷ�ݳ�ȥ�ϰࣿ��˵�����ɣ�