题目内容
已知如图,矩形OABC的长OA=![]() ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.
(1)求∠PCB的度数;
(2)若P,A两点在抛物线y=-![]() x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
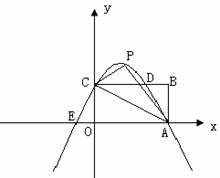
(1)∠PCB=30°
(2)![]()
点C(0,1)满足上述函数关系式,所以点C在抛物线上.
(3)Ⅰ、若DE是平行四边形的对角线,点C在y轴上,CD平行x轴,
∴过点D作DM∥ CE交x轴于M,则四边形EMDC为平行四边形,
把y=1代入抛物线解析式得点D的坐标为(![]() ,1)
,1)
把y=0代入抛物线解析式得点E的坐标为(![]() ,0)
,0)
∴M(![]() ,0);N点即为C点,坐标是(0,1);
,0);N点即为C点,坐标是(0,1);
Ⅱ、若DE是平行四边形的边,
则DE=2,∠DEF=30°,
过点A作AN∥DE交y轴于N,四边形DANE是平行四边形,
∴M(![]() ,0),N(0,-1); …
,0),N(0,-1); …
同理过点C作CM∥DE交y轴于N,四边形CMDE是平行四边形,
∴M(![]() ,0),N(0, 1).
,0),N(0, 1).

练习册系列答案
相关题目
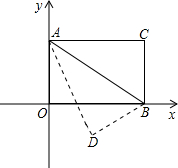 B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.
B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.


