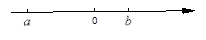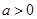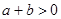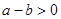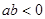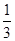题目内容
(本题12分) 如果一个正整数能够表示为两个连续的偶数的平方差,那么称这个正整数为“神秘数”.如4=22-02;12=42-22;20=62-42.因此4、12、20这三个数都是神秘数.
(1)请你写出50以内的两个神秘数(除4、12、20外),并判断2012是否是神秘数?(不要说明理由)
(2)设两个连续偶数为2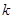 +2和2
+2和2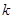 (其中
(其中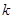 为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
(3)试说明:两个连续奇数的平方差(取正数)不是神秘数.
(1)请你写出50以内的两个神秘数(除4、12、20外),并判断2012是否是神秘数?(不要说明理由)
(2)设两个连续偶数为2
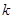 +2和2
+2和2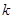 (其中
(其中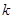 为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.(3)试说明:两个连续奇数的平方差(取正数)不是神秘数.

解:(1)根据题意,得
 ……
……
所以50以内的神秘数有28,36等。
设 ,解得k=251
,解得k=251
即 所以2012是神秘的数。
所以2012是神秘的数。
(2)因为 所以由两个连续偶数2k+2和2k的平方差构成的神秘数是4的倍数。
所以由两个连续偶数2k+2和2k的平方差构成的神秘数是4的倍数。
(3)设2k+1和2k-1是两个连续的奇数,则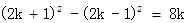
即两个连续的奇数的平方差是8的倍数,所以肯定是4的倍数,根据(2)的结论是4的倍数就可以写成两个连续偶数的平方差,所以两个连续奇数的平方差也是神秘的数。

 ……
……所以50以内的神秘数有28,36等。
设
 ,解得k=251
,解得k=251即
 所以2012是神秘的数。
所以2012是神秘的数。(2)因为
 所以由两个连续偶数2k+2和2k的平方差构成的神秘数是4的倍数。
所以由两个连续偶数2k+2和2k的平方差构成的神秘数是4的倍数。(3)设2k+1和2k-1是两个连续的奇数,则
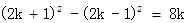
即两个连续的奇数的平方差是8的倍数,所以肯定是4的倍数,根据(2)的结论是4的倍数就可以写成两个连续偶数的平方差,所以两个连续奇数的平方差也是神秘的数。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
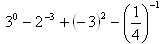 (2)
(2) 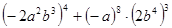
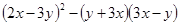 (4)
(4) 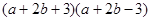
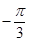 、-0.95、
、-0.95、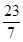 、0、
、0、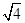 、0.121121112…、
、0.121121112…、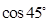 、
、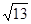 、
、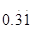 无理数的个数为( )
无理数的个数为( ) , 接收方由
, 接收方由 的相反数是( )
的相反数是( )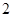
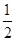

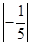 ,
,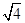 ,
,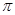 ,
,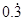 , ,
, ,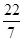 中无理数有几个
中无理数有几个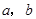 在数轴上的位置如图所示,下列各式正确的是( )
在数轴上的位置如图所示,下列各式正确的是( )