题目内容
 在直径为50cm的圆中,弦AB为40cm,弦CD为48cm,且AB∥CD,求AB与CD之间距离.
在直径为50cm的圆中,弦AB为40cm,弦CD为48cm,且AB∥CD,求AB与CD之间距离.
解:如图所示,过O作OM⊥AB,
∵AB∥CD,∴ON⊥CD.
在Rt△BMO中,BO=25cm.
由垂径定理得BM= AB=
AB= ×40=20cm,
×40=20cm,
∴OM=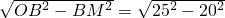 =15cm.
=15cm.
同理可求ON=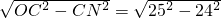 =7cm,
=7cm,
所以MN=OM-ON=15-7=8cm.
以上解答有无漏解,漏了什么解,请补上.
 解:有漏解.
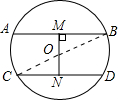
解:有漏解.当两弦位于圆心的两旁时,如图所示:
过O作OM⊥AB,
∵AB∥CD,∴ON⊥CD.
在Rt△BMO中,BO=25cm.
由垂径定理得BM=
 AB=
AB= ×40=20cm,
×40=20cm,∴OM=
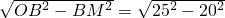 =15cm.
=15cm.同理可求ON=
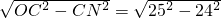 =7cm,
=7cm,则MN=OM+ON=15+7=22(cm).
分析:在解题的过程中要环环相扣,不能漏掉必要的环节.根据上述步骤有漏解的步骤就是MN的长度.
点评:主要考查了垂径定理的运用.垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.
分类讨论训练学生思维的严谨性.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
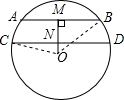 在直径为50cm的圆中,弦AB为40cm,弦CD为48cm,且AB∥CD,求AB与CD之间距离.
在直径为50cm的圆中,弦AB为40cm,弦CD为48cm,且AB∥CD,求AB与CD之间距离.