��Ŀ����
2��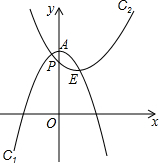 ��ͼ����A����E������ֱ�Ϊ ��0��3���루1��2�����Ե�AΪ�����������ΪC1��y1=-x2+n����EΪ�����������ΪC2��y2=ax2+bx+c����������C2��y�ύ�ڵ�P��0��$\frac{5}{2}$����
��ͼ����A����E������ֱ�Ϊ ��0��3���루1��2�����Ե�AΪ�����������ΪC1��y1=-x2+n����EΪ�����������ΪC2��y2=ax2+bx+c����������C2��y�ύ�ڵ�P��0��$\frac{5}{2}$������1���ֱ����������C1��C2�Ľ���ʽ�����ж�������C1�ᾭ����E��
��2����������C1��C2�е�y����x���������С����ֱ��д����ʱx��ȡֵ��Χ��
��3���ڣ�2����x��ȡֵ��Χ�ڣ����µĺ���y3=y1-y2���������y3��x�ĺ�����ϵʽ���ʵ�xΪ��ֵʱ������y3�����ֵ�����������ֵ��
���� ��1������ϵ�����ֱ����ɵã������x=1ʱ��y1��ֵ�����ж�������C1�Ƿ���E��
��2���ֱ����������y��x���������Сʱx�ķ�Χ�ɵô𰸣�
��3����y1��y2����y3=y1-y2������һ��ʽ�����䷽�ɶ���ʽ�ɵô𰸣�
��� �⣺��1���������⽫��A��0��3������y1=-x2+n���ã�n=3��
��y1=-x2+3��
��������C2�Ķ�������Ϊ��1��2����
����������C2�Ľ���ʽΪy=a��x-1��2+2��
����P��0��$\frac{5}{2}$�����룬�ã�a+2=$\frac{5}{2}$��
��ã�a=$\frac{1}{2}$��
��������C2�Ľ���ʽΪy2=$\frac{1}{2}$��x-1��2+2=$\frac{1}{2}$x2-x+$\frac{5}{2}$��
��x=1ʱ��y1=-12+3=2��
��������C1������E��
��2����y1=-x2+3����x��0ʱ��y��x���������С��
��y2=$\frac{1}{2}$��x-1��2+2�У���x��1ʱ��y��x���������С��
�൱0��x��1ʱ��������C1��C2�е�y����x���������С��
��3��y3=y1-y2=-x2+3-��$\frac{1}{2}$x2-x+$\frac{5}{2}$��=-$\frac{3}{2}$x2+x+$\frac{1}{2}$=-$\frac{3}{2}$��x-$\frac{1}{3}$��2+$\frac{2}{3}$��
��0��x��1��
�൱x=$\frac{1}{3}$ʱ������y3�����ֵ�����ֵΪ$\frac{2}{3}$��
���� ���⿼���˴���ϵ��������κ�������ʽ�����κ��������ʣ��������մ���ϵ�����Ͷ��κ������������ǽⱾ��Ĺؼ���

| A�� | ������������ͳ��Ϊ���� | B�� | 0��������Ҳ�Ǹ����� | ||
| C�� | ��������������ͳ��Ϊ���� | D�� | ��������ͳ��Ϊ������ |
 ��ͼ��У����һ������洹ֱ��������ѧ��ȤС�����β������ڵ����ϵ�Ӱ�ӣ���һ��������������60���ʱ���ڶ���������������30���ʱ�����β�����Ӱ�����8�ף�������AB�����ף�������������ţ�
��ͼ��У����һ������洹ֱ��������ѧ��ȤС�����β������ڵ����ϵ�Ӱ�ӣ���һ��������������60���ʱ���ڶ���������������30���ʱ�����β�����Ӱ�����8�ף�������AB�����ף�������������ţ�