��Ŀ����
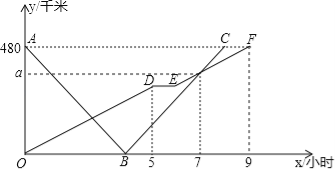
����Ŀ������������12�֣��졢�������ֱ�����480ǧ��·�̵ļס�������ͬʱ������������ʻ����������У�;���������ͣ��1Сʱ��Ȼ����ԭ�ټ��������ʻ������غ�ֹͣ��ʻ���쳵�����ҵغ�������ԭ·ԭ�ٷ��ؼأ��쳵��ͷ��ʱ����Բ��ƣ����졢���������ҵص�·��![]() ��ǧ�ף�������ʱ��
��ǧ�ף�������ʱ��![]() ��Сʱ��֮��ĺ���ͼ����ͼ������ͼ����Ϣ����������⣺
��Сʱ��֮��ĺ���ͼ����ͼ������ͼ����Ϣ����������⣺
��1������������ʻ�ٶȺ�![]() ��ֵ��
��ֵ��
��2����쳵��������һ������ʱ������ص�·���Ƕ���ǧ�ף�
��3��������������Сʱ����·��Ϊ![]() ǧ�ף�
ǧ�ף�
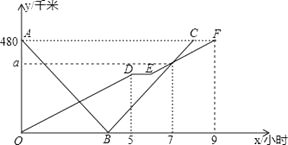
���𰸡���1��60ǧ��/ʱ,360;��2��320ǧ��;��3��![]() ��
��![]() ��
��![]() Сʱ
Сʱ
�������������������1�����ٶ�=·����ʱ�伴�ɵó��������ٶȣ�a����Ӧ��ʱ��Ϊ7����·��=�ٶ���ʱ�䣬�ɵó�a��ֵ��
��2��������ʱ��Ϊt�����ͼ������쳵���ٶȣ���������ʱ��=���ؾ����������ٶ�֮�ͣ��ɵó�����ʱ�䣬����·��=�ٶ���ʱ�伴�ɵó����ۣ�
��3����Ͽ������ٶ������ؾ��룬�ҳ�B��C��D��E������꣬���߶��ϵ�����������ҳ����߶εĽ���ʽ������·�����=160�����ҳ����ۣ�
�⣺��1����������ʻ�ٶ�Ϊ480����9��1��=60��ǧ��/ʱ����
a=��7��1����60=360��
��2���쳵����ʻ�ٶ�Ϊ��480+360����7=120��ǧ��/ʱ����
����������ʱ��Ϊ480����60+120��=![]() ��Сʱ����
��Сʱ����
120��![]() =320��ǧ�ף���
=320��ǧ�ף���
�𣺿쳵��������һ������ʱ������ص�·����320ǧ�ף�
��3��480��120=4��Сʱ����
��B��������4��0����
4��2=8��Сʱ����
��C��������8��480����
60��5=300��ǧ�ף���
��D��������5��300����E��������6��300����
���ͼ�ο�֪��AB��y=��120x+180��0��x��4����BC��y=120x��480��4��x��8����OD��y=60x��0��x��5����DE��y=300��5��x��6����EF��y=60x��60��7��x��9����
����120x+180��60x=160�����x=![]() ��
��
��60x������120x+180��=160�����x=![]() ��
��
��300������120x+180��=160�����x=![]() ��
��
��120x��480����60x��60��=160�����x=![]() ����ȥ����
����ȥ����
�ʣ�����������![]() ��
��![]() ��
��![]() Сʱ����·��Ϊ160ǧ�ף�
Сʱ����·��Ϊ160ǧ�ף�