Question

【题目】如图，直线是足球场的底线，是球门，点是射门点，连接，叫做射门角.

（1）如图，点是射门点，另一射门点在过三点的圆外（未超过底线）.证明：

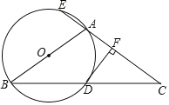
（2）如图，经过球门端点，直线，垂足为且与相切与点，于点，连接，若，求此时一球员带球沿直线向底线方向运球时最大射门角的度数．

Answer 1

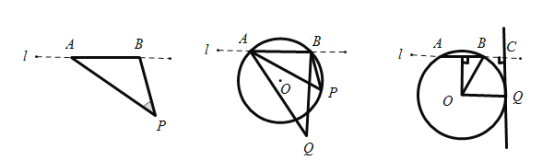
【答案】（1）证明见解析；（2）

【解析】

（1）由同弧所对的圆周角相等可得：∠ACB=∠APB，再根据三角形外角大于不相邻的内角即可解答；

（2）由垂径定理可得AE=EB=AB，∠EOB=∠AOB；在Rt△OBE中，再由OB =2a，EB= a，可得∠EOB=30°，∠AOB=2∠EOB=60°，根据圆周角定理可得结果.

解：（1）证明：

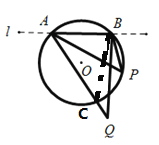
连接BC，∵∠ACB=∠APB（同弧所对的圆周角相等）

∠ACB（三角形外角大于不相邻的内角）

∴

（2）当球员运动到点Q时，射门角最大．

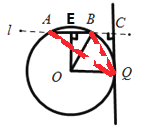
∵OE⊥AB,

∴AE=EB=AB=×2a=a，EC=EB+BC=2a，∠EOB=∠AOB

连接AQ、BQ，由题意得四边形OQCE是矩形，OQ=EC=2a=OB，

Rt△OBE中，∵OB =2a，EB= a

∴∠EOB=30°，∠AOB=2∠EOB=60°

∴∠AQB=∠AOB=30°.