题目内容
【题目】(1)两条直线相交于一点有2组不同的对顶角;
(2)三条直线相交于一点有6组不同的对顶角;
(3)四条直线相交于一点有12组不同的对顶角;
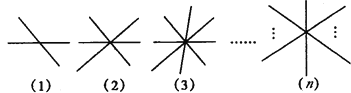
(4)n条直线相交于同一点有___________组不同对顶角.(如图所示)
【答案】n(n-1)
【解析】因为两条直线相交于一点有2组不同的对顶角;三条直线相交于一点有6组不同的对顶角;四条直线相交于一点有12组不同的对顶角;n条直线相交时,这个图形的对顶角的个数是:n(n-1)对对顶角.
解:(1)2条直线相交于一点有2×1=2组不同的对顶角;
(2)3条直线相交于一点有3×2=6组不同的对顶角;
(3)4条直线相交于一点有4×3=12组不同的对顶角;
按照以上规律可得:
(4)n条直线相交于一点有n(n-1)组不同的对顶角.
“点睛”本题是一个探索规律型的题目,解决时注意观察每对数之间的关系.这是中考中经常出现的问题.

练习册系列答案
相关题目