题目内容
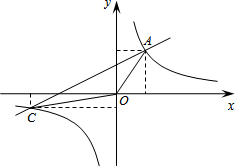 如图直线AC与函数y=
如图直线AC与函数y=| m | x |
①求直线AC的解析式和m的值;
②求△AOC的面积.
分析:(1)先把A点坐标代入y=
求出m的值,确定反比例函数解析式,再利C点的纵坐标为-1确定C点坐标,然后利用待定系数法求直线AC的解析式;
(2)先确定直线AC与y轴的交点坐标,然后根据三角形面积公式和S△AOC=S△BOC+S△BOA进行计算.
| m |
| x |
(2)先确定直线AC与y轴的交点坐标,然后根据三角形面积公式和S△AOC=S△BOC+S△BOA进行计算.
解答:解:(1)把A(2,3)代入y=
得m=2×3=6,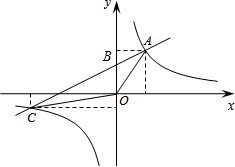
∴反比例函数解析式为y=
,
把y=-1代入y=
得x=-6,
∴C点坐标为(-6,-1),
设直线AC的解析式为y=kx+b,
把A(2,3)、C(-6,-1)代入得
,
解得
,
∴直线AC的解析式为y=
x+2;
(2)如图,当x=0时,y=
x+2=2,则B点坐标为(0,2),
S△AOC=S△BOC+S△BOA=
×2×6+
×2×2=8.
| m |
| x |

∴反比例函数解析式为y=
| 6 |
| x |
把y=-1代入y=
| 6 |
| x |
∴C点坐标为(-6,-1),
设直线AC的解析式为y=kx+b,
把A(2,3)、C(-6,-1)代入得
|
解得
|
∴直线AC的解析式为y=
| 1 |
| 2 |
(2)如图,当x=0时,y=
| 1 |
| 2 |
S△AOC=S△BOC+S△BOA=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函图象与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法确定函数解析式以及三角形面积公式.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 已知反比例函数
已知反比例函数 (2012•湖里区一模)如图,反比例函数y=
(2012•湖里区一模)如图,反比例函数y= 已知反比例函数
已知反比例函数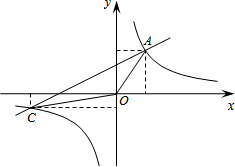 如图直线AC与函数
如图直线AC与函数 的图象交于A、C两点,A(2,3),C点的纵坐标为-1,O为坐标原点.
的图象交于A、C两点,A(2,3),C点的纵坐标为-1,O为坐标原点.