题目内容
【题目】如图，将一张长方形大铁皮切割成九块，切痕如图虚线所示，其中有两块是边长都为xdm的大正方形，两块是边长都为ydm的小正方形，五块是长宽分别是xdm、ydm的全等小长方形，且x＞y．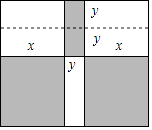
（1）用含x、y的代数式表示长方形大铁皮的周长为 dm；
（2）若每块小长方形的面积10dm2 ， 四个正方形的面积为58dm2 ， 试求该切痕的总长．
【答案】
（1）（6x+6y）
（2）
解：由题意可知：xy=10，2x2+2y2=58，
即：x2+y2=29，
∵（x+y）2=x2+2xy+y2=29+20=49
∴x+y=7，
∴切痕总长为6×7=42dm
【解析】（1）根据题意得：长方形大铁皮的周长为6x+6y（cm）；
所以答案是：（6x+6y）；
练习册系列答案
名校通行证有效作业系列答案
相关题目
