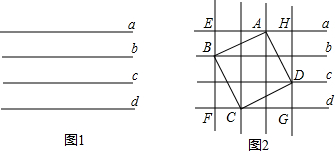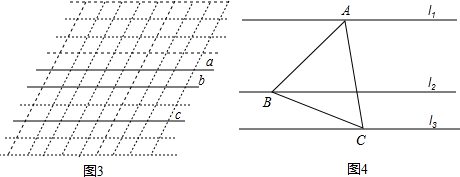题目内容
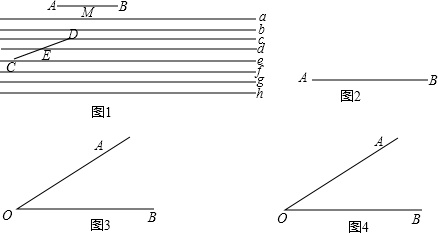
小明利用等距平行线解决了二等分线段的问题.
作法:
(1)在e上任取一点C,以点C为圆心,AB长为半径画弧交c于点D,交d于点E;
(2)以点A为圆心,CE长为半径画弧交AB于点M;
∴点M为线段AB的二等分点.
解决下列问题:(尺规作图,保留作图痕迹)
(1)仿照小明的作法,在图2中作出线段AB的三等分点;
(2)点P是∠AOB内部一点,过点P作PM⊥OA于M,PN⊥OB于N,请找出一个满足下列条件的点P.(可以利用图1中的等距平行线)
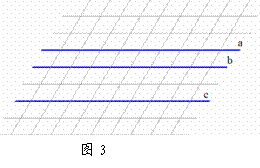
①在图3中作出点P,使得PM=PN; ②在图4中作出点P,使得PM=2PN.

作法:
(1)在e上任取一点C,以点C为圆心,AB长为半径画弧交c于点D,交d于点E;
(2)以点A为圆心,CE长为半径画弧交AB于点M;
∴点M为线段AB的二等分点.
解决下列问题:(尺规作图,保留作图痕迹)
(1)仿照小明的作法,在图2中作出线段AB的三等分点;
(2)点P是∠AOB内部一点,过点P作PM⊥OA于M,PN⊥OB于N,请找出一个满足下列条件的点P.(可以利用图1中的等距平行线)
①在图3中作出点P,使得PM=PN; ②在图4中作出点P,使得PM=2PN.

分析:(1)作法:①在e上任取一点C,以点C为圆心,AB长为半径画弧交b于点D,交d于点E,交c于点F;②以点A为圆心,CE长为半径画弧交AB于点P1,再以点B为圆心,CE长为半径画弧交AB于点P2;则点P1、P2为线段AB的三等分点;
(2)①以O为圆心,任意长为半径画弧,交OA于G,交OB于H;在d上任取一点C,以点C为圆心,GH长为半径画弧交b于点D,交c于点E;以点G为圆心,CE长为半径画弧交GH于点P;则P点为所求;
②以O为圆心,任意长为半径画弧,交OA于G,交OB于H;在d上任取一点C,以点C为圆心,GH长为半径画弧交a于点D,交c于点E,交b于点F;②以点G为圆心,CF长为半径画弧交GH于点P;则则P点为所求.
(2)①以O为圆心,任意长为半径画弧,交OA于G,交OB于H;在d上任取一点C,以点C为圆心,GH长为半径画弧交b于点D,交c于点E;以点G为圆心,CE长为半径画弧交GH于点P;则P点为所求;
②以O为圆心,任意长为半径画弧,交OA于G,交OB于H;在d上任取一点C,以点C为圆心,GH长为半径画弧交a于点D,交c于点E,交b于点F;②以点G为圆心,CF长为半径画弧交GH于点P;则则P点为所求.
解答:解:(1)如下图所示,点P1、P2为线段AB的三等分点;

(2)①如下图所示,点P即为所求;
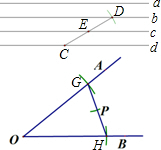
②如下图所示,点P即为所求.
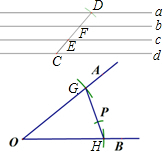

(2)①如下图所示,点P即为所求;

②如下图所示,点P即为所求.

点评:本题考查了作图-应用与设计作图,学生的阅读理解能力及知识的迁移能力,理解等距平行线的含义及平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目