题目内容
(2013•海淀区一模)问题:如图1,a、b、c、d是同一平面内的一组等距平行线(相邻平行线间的距离为1).画出一个正方形ABCD,使它的顶点A、B、C、D分别在直线a、b、d、c上,并计算它的边长.
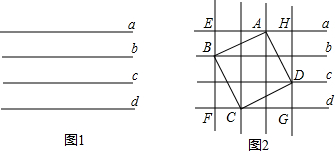
小明的思考过程:
他利用图1中的等距平行线构造了3×3的正方形网格,得到了辅助正方形EFGH,如图2所示,再分别找到它的四条边的三等分点A、B、C、D,就可以画出一个满足题目要求的正方形.
请回答:图2中正方形ABCD的边长为
.
请参考小明的方法,解决下列问题:
(1)请在图3的菱形网格(最小的菱形有一个内角为60°,边长为1)中,画出一个等边△ABC,使它的顶点A、B、C落在格点上,且分别在直线a、b、c上;
(3)如图4,l1、l2、l3是同一平面内的三条平行线,l1、l2之间的距离是
,l2、l3之间的距离是
,等边△ABC的三个顶点分别在l1、l2、l3上,直接写出△ABC的边长.
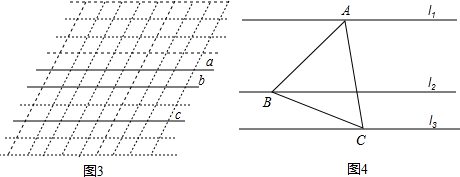
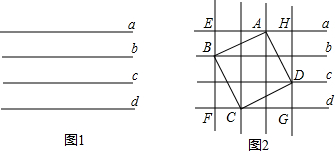
小明的思考过程:
他利用图1中的等距平行线构造了3×3的正方形网格,得到了辅助正方形EFGH,如图2所示,再分别找到它的四条边的三等分点A、B、C、D,就可以画出一个满足题目要求的正方形.
请回答:图2中正方形ABCD的边长为
| 5 |
| 5 |
请参考小明的方法,解决下列问题:
(1)请在图3的菱形网格(最小的菱形有一个内角为60°,边长为1)中,画出一个等边△ABC,使它的顶点A、B、C落在格点上,且分别在直线a、b、c上;
(3)如图4,l1、l2、l3是同一平面内的三条平行线,l1、l2之间的距离是
| 21 |
| 5 |
| 21 |
| 10 |
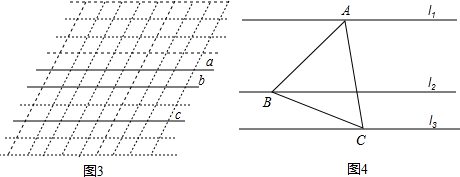
分析:(1)直接运用勾股定理就可以求出AB的值;
(2)根据等边三角形的性质就可以画出符合条件的图形;
(3)过点B作DE⊥l3于E,交l1于D,作CF⊥l1于点F,设AD=x,AF=y,根据勾股定理建立方程组求出其解即可.
(2)根据等边三角形的性质就可以画出符合条件的图形;
(3)过点B作DE⊥l3于E,交l1于D,作CF⊥l1于点F,设AD=x,AF=y,根据勾股定理建立方程组求出其解即可.
解答:解:(1)由题意,得
AE=2,BE=1,在Rt△ABE中,由勾股定理,得
AB=
.
故答案为:
(2)根据条件画出图形为如图3: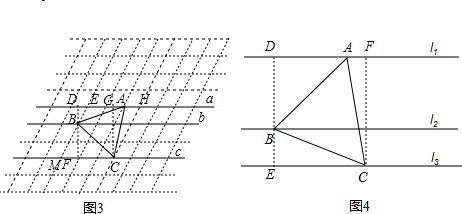
作垂BD⊥a与D,BF⊥c于F,CG⊥a于G,
∵∠DEB=∠BMF=∠GHC=60°,BE=1,BM=2,CH=3,
∴DE=0.5,MF=1,GH=1.5,
∴AD=2.5,FC=2,AG=0.5,
∴BD=
,BF=
,CG=
,
∴在Rt△BDG、Rt△BFC和Rt△AGC中,由勾股定理,得
AB=
=
,
BC=
=
,
AC=
=
,
∴AB=BC=AC,
∴△ABC是等边三角形;
(3)如图4,过点B作DE⊥l3于E,交l1于D,作CF⊥l1于点F,
∴∠BEC=∠AFC=90°.
∵l1∥l3,
∴∠BEC+∠ADE=180°,
∴∠ADB=90°.
∵三角形ABC是等边三角形,
∴AB=BC=AC.
设AD=x,AF=y,
,
由②-①,得
y2-x2+
=0,
20y2-20x2+441=0,
40y2-40x2+882=0 ④.
由②-③,得
-25x2-50xy+882=0 ⑤
由④-⑤,得
8y2+10xy-3x2=0.
(4y-x)(2y+3x)=0,
∴x=4y或x=-
y.
∵x>0,y>0,
∴x=-
y(舍去),
∴x=4y.
∴20y2-20(4y)2+441=0,
∴y2=
,
+
=AC2,
∴AC=
.
答:△ABC的边长为
.
AE=2,BE=1,在Rt△ABE中,由勾股定理,得
AB=
| 5 |
故答案为:
| 5 |
(2)根据条件画出图形为如图3:

作垂BD⊥a与D,BF⊥c于F,CG⊥a于G,
∵∠DEB=∠BMF=∠GHC=60°,BE=1,BM=2,CH=3,
∴DE=0.5,MF=1,GH=1.5,
∴AD=2.5,FC=2,AG=0.5,
∴BD=
| ||
| 2 |
| 3 |
3
| ||
| 2 |
∴在Rt△BDG、Rt△BFC和Rt△AGC中,由勾股定理,得
AB=
|
| 7 |
BC=
| 3+4 |
| 7 |
AC=
|
| 7 |
∴AB=BC=AC,
∴△ABC是等边三角形;
(3)如图4,过点B作DE⊥l3于E,交l1于D,作CF⊥l1于点F,
∴∠BEC=∠AFC=90°.
∵l1∥l3,
∴∠BEC+∠ADE=180°,
∴∠ADB=90°.
∵三角形ABC是等边三角形,
∴AB=BC=AC.
设AD=x,AF=y,
|
由②-①,得
y2-x2+
| 441 |
| 20 |
20y2-20x2+441=0,
40y2-40x2+882=0 ④.
由②-③,得
-25x2-50xy+882=0 ⑤
由④-⑤,得
8y2+10xy-3x2=0.
(4y-x)(2y+3x)=0,
∴x=4y或x=-
| 2 |
| 3 |
∵x>0,y>0,
∴x=-
| 2 |
| 3 |
∴x=4y.
∴20y2-20(4y)2+441=0,
∴y2=
| 147 |
| 100 |
| 147 |
| 100 |
| 3969 |
| 100 |
∴AC=
| 7 |
| 5 |
| 21 |
答:△ABC的边长为
| 7 |
| 5 |
| 21 |
点评:本题考查了勾股定理的运用,等边三角形的判定及性质的运用,列二元二次方程组解实际问题的运用及二元二次方程组的解法的运用,直角三角形的性质的运用,解答时灵活运用勾股定理建立方程是关键.

练习册系列答案
相关题目
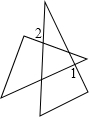 (2013•海淀区一模)一副三角板如图放置,若∠1=90°,则∠2的度数为( )
(2013•海淀区一模)一副三角板如图放置,若∠1=90°,则∠2的度数为( )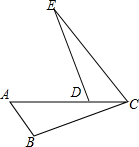 (2013•海淀区一模)已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.
(2013•海淀区一模)已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.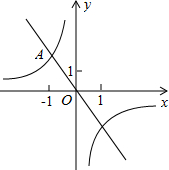 (2013•海淀区一模)如图,在平面直角坐标系xOy中,反比例函数
(2013•海淀区一模)如图,在平面直角坐标系xOy中,反比例函数