题目内容
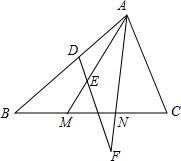 如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求证:EF=3DE.
如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求证:EF=3DE.
分析:过N、M分别作AC的平行线,由线段之间的关系可得
=
,进而由DF∥HN,可得
=
=
,即
=
,进而即可得出结论.
| HK |
| KN |
| 1 |
| 3 |
| HK |
| DE |
| AK |
| AE |
| KN |
| EF |
| DE |
| EF |
| HK |
| KN |
解答: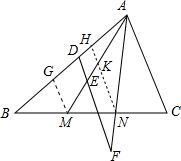 证明:过N、M分别作AC的平行线交AB于H,G 两点,NH交AM于K,
证明:过N、M分别作AC的平行线交AB于H,G 两点,NH交AM于K,
∵BM=MN=NC,
∴BG=GH=HA,
则HK=
GM,GM=
HN,
∴HK=
HN,即
=
,
又DF∥HN,
∴
=
=
,
即EF=3DE.
 证明:过N、M分别作AC的平行线交AB于H,G 两点,NH交AM于K,
证明:过N、M分别作AC的平行线交AB于H,G 两点,NH交AM于K,∵BM=MN=NC,
∴BG=GH=HA,
则HK=
| 1 |
| 2 |
| 1 |
| 2 |
∴HK=
| 1 |
| 4 |
| HK |
| KN |
| 1 |
| 3 |
又DF∥HN,
∴
| DE |
| EF |
| HK |
| KN |
| 1 |
| 3 |
即EF=3DE.
点评:本题主要考查了平行线分线段成比例的性质,能够熟练运用其性质求解一些简单的计算、证明问题.

练习册系列答案
相关题目
 P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.
P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts. 如图,已知E、F分别为矩形ABCD的边BA、DC的延长线上的点,且AE=
如图,已知E、F分别为矩形ABCD的边BA、DC的延长线上的点,且AE= 如图,已知⊙P的半径为1,圆心P在抛物线
如图,已知⊙P的半径为1,圆心P在抛物线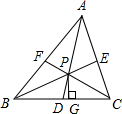 如图,已知△ABC,P为内角平分线AD,BE,CF的交点,过点P作PG⊥BC于G,试说明∠BPD与∠CPG的大小关系,并说明理由.
如图,已知△ABC,P为内角平分线AD,BE,CF的交点,过点P作PG⊥BC于G,试说明∠BPD与∠CPG的大小关系,并说明理由. 如图,已知长方形的长为a,宽为b,且a>b,则阴影部分的面积用代数式表示为
如图,已知长方形的长为a,宽为b,且a>b,则阴影部分的面积用代数式表示为