��Ŀ����
��ͼ��ʾ��ijУ�ƻ���һ����״Ϊ���������ABC�Ŀյؽ�����̬�������죮��֪��ABC�ı�BC��120�ף���AD��80�ף�ѧУ�ƻ������ָ�ɡ�AHG����BHE����GFC�;���EFGH�IJ��֣���ͼ�������о���EFGH��һ��EF�ڱ�BC�ϣ�������������H��G�ֱ��ڱ�AB��AC�ϣ��ּƻ��ڡ�AHG���ֲݣ�ÿƽ����Ͷ��6Ԫ���ڡ�BHE����FCG�϶��ֻ���ÿƽ����Ͷ��10Ԫ���ھ���EFGH���˽�������أ�ÿƽ����Ͷ��4Ԫ��
��1����FG��Ϊ������ʱ���ֲݵ�������ֻ��������ȣ�
��2��������EFGH�ı�FGΪ������ʱ����ABC�յظ�����Ͷ����С����СֵΪ���٣�
��1��40����2��FG=60ʱ����ABC�յظ�����Ͷ����С����СֵΪ26400��
���������������1�����������Ʒֱ��ʾ����Ӧ�������εĵ���ߣ��������ȼ��ɣ�
��2������Ӧ����Ͷ���ú�x�Ĵ���ʽ��ʾ����������κ�������ֵ���ɣ�
�����������1����FG=x�ף���AK=��80��x���ף�
�ɡ�AHG�ס�ABC��BC=120��AD=80���ɵã� ����HG=
����HG=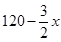 ��BE+FC=120����
��BE+FC=120����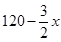 ��=
��=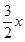 ����
����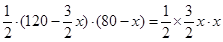 �����
����� ���൱FG�ij�Ϊ40��ʱ���ֲݵ�������ֻ��������ȣ�
���൱FG�ij�Ϊ40��ʱ���ֲݵ�������ֻ��������ȣ�
��2�����������Ͷ��ΪWԪ��
��W=
= ��
��
�߶�����ϵ��6��0��0��x��80���൱x=20ʱ��W��С=26400��
�𣺵�����EFGH�ı�FG��Ϊ20��ʱ���յظ������Ͷ����С����СֵΪ26400Ԫ��
���㣺1�����κ�����Ӧ�ã�2�����ε����ʣ�3�����������ε�Ӧ�ã�

 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�

 Ϊ��ֵʱ����BPQΪֱ�������Σ�
Ϊ��ֵʱ����BPQΪֱ�������Σ�
 DC������
DC������ ���ӳ���
���ӳ��� ���ӳ����ڵ�
���ӳ����ڵ�





 =t������t��ʾEF�ij���
=t������t��ʾEF�ij���