题目内容
如图,在平面直角坐标系中,A(a,0),B(b,0),C(-2,1),且|a+2b+1|+(3a-4b+13)2=0.

(1)求a,b的值;
(2)在y轴上存在一点D,使得△COD的面积是△ABC面积的两倍,求出点D的坐标.
(3)在x轴上是否存在这样的点,存在请直接写出点D的坐标,不存在请说明理由.

(1)求a,b的值;
(2)在y轴上存在一点D,使得△COD的面积是△ABC面积的两倍,求出点D的坐标.
(3)在x轴上是否存在这样的点,存在请直接写出点D的坐标,不存在请说明理由.
(1)a=-3,b=1;(2)(0,4),(0,-4); (3)(8,0),(-8,0)
试题分析:依题意知b+1|+(3a-4b+13)2=0.则
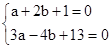 解得a=-3,b=1
解得a=-3,b=1(2)由(1)知A(-3,0)B(1,0)C(-2,1)
所以S△ABC=
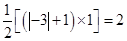
设y轴存在点D使得△COD的面积是△ABC面积的两倍。则S△COD=4
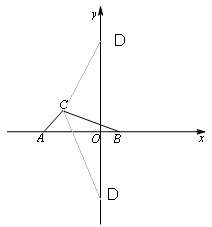
则设OD=d,△COD高是2。则d=4×2÷2=4.
故点D坐标:(0,4),(0,-4);
(3)同理可证,设x轴上存在点D使得△COD的面积是△ABC面积的两倍。则S△COD=4
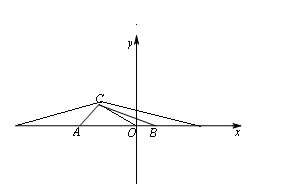
底边DO=d。△COD高是1。
则d=4×2÷1="8." 故点D坐标:(8,0),(-8,0)
点评:本题难度中等,主要考查学生对直角坐标系求面积等综合运用能力。为中考常考题型,要求学生牢固掌握解题技巧。

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 中自变量x的取值范围是 .
中自变量x的取值范围是 .
 上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=9.则k的值是
上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=9.则k的值是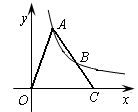

 轴的负方向平移6个单位,它与点 重合。
轴的负方向平移6个单位,它与点 重合。 轴是什么关系?
轴是什么关系? ,则点A(
,则点A( ,
, ) ( )
) ( ) 中自变量x的取值范围是 .
中自变量x的取值范围是 . 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .