��Ŀ����
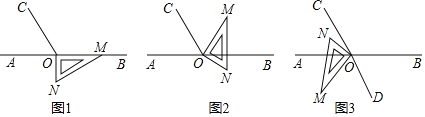
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC��120�㣮��һֱ�������ε�ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
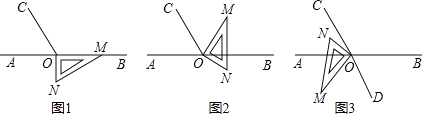
��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC���ʣ�ֱ��ON�Ƿ�ƽ�֡�AOC����˵�����ɣ�
��2����ͼ1�е����ǰ��Ƶ�O��ÿ��5����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���t��ʱ��ֱ��ONǡ��ƽ����ǡ�AOC����t��ֵΪ�� ��ֱ��д���������
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON�ڡ�AOC���ڲ���ODΪ��BOMƽ���ߣ���̽������MOD���NOC֮���������ϵ����˵�����ɣ�
���𰸡���1������������2��12����48������3��2��MOD+��NOC=150�������ɼ�����.
��������
��1����ͼ2�У���ON�ķ����ӳ���ΪOD��������ǵ����ʺͶԶ��ǵ����ʿ�֤����COD=��AOD��
��2�����������ηֱ����̼��ɽ�����⣻
��3�����ۣ���AOM=��NOC+30�������ݽǵĺͲ���жϼ��ɣ�
��1���⣺ֱ��ONƽ����AOC����ON�ķ����ӳ���ΪOD��
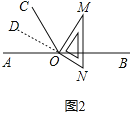
��OMƽ����BOC��
���MOC����MOB��
����OM��ON��
���MOD����MON��90����
���COD����BON��
���ߡ�AOD����BON��
���COD����AOD��
��ֱ��ONƽ����AOC��
��2���⣺������5t��60����5t��240����
���t��12��48��
�ʴ�Ϊ12���48�룮
��3���⣺���ۣ���AOM����NOC+30����
���ɣ��ߡ�MON��90������AOC��60����
���AOM��90������AON����NOC��60������AON��
���AOM����NOC����90������AON������60������AON����30����
����AOM����NOC+30����
��ODΪ��BOMƽ����,
���BOM=2��MOD,
�ߡ�AOM+��BOM=180��,
���AOM=180��-2��MOD,
��180��-2��MOD=��NOC+30��,
��2��MOD+��NOC=150��.

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�����Ŀ��Ϊ����������У��ס������ҹ�˾�Ƴ�ר�������˼��շ����£�����ʻ·��![]() ʱ���ú�
ʱ���ú�![]() �Ĵ���ʽ��ʾ�ҹ�˾���˼�.
�Ĵ���ʽ��ʾ�ҹ�˾���˼�.
��ʻ·�� | �շѱ� | |
�� | �� | |
������ | ��6Ԫ | ��7Ԫ |
���� | ÿ����2.1Ԫ | ÿ����1.6Ԫ |
���� | ÿ����2.2Ԫ | |
��1����![]() ʱ������ñ�ʾΪ Ԫ����
ʱ������ñ�ʾΪ Ԫ����![]() ʱ������ñ�ʾΪ Ԫ.
ʱ������ñ�ʾΪ Ԫ.
��2������ʻ·��![]() ʱ�����ڳ˿���˵���ĸ�ר�������㣬Ϊʲô��
ʱ�����ڳ˿���˵���ĸ�ר�������㣬Ϊʲô��
��3������ʻ·��![]() ʱ�����ڳ˿���˵���ĸ�ר�������㣬Ϊʲô��
ʱ�����ڳ˿���˵���ĸ�ר�������㣬Ϊʲô��