Question

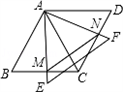
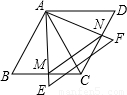
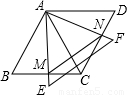
如图所示，两个同样大小的等边△ABC和△ACD，边长为12，它们拼成一个菱形ABCD，另一个足够大等边△AEF绕点A旋转，AE与BC相交于点M，AF与CD相交于点N．
（1）判断AM与AN是否相等，并简要说明理由；
（2）求四边形AMCN的面积；
（3）探索△AMN何时面积最小，并求出这个最小面积．

Answer 1

分析：（1）AM=AN，先证明△ACN≌△ABM，再根据全等三角形的对应边相等的性质得出答案；
（2）先证明S_△ABC=S_{四边形AMCN}，再用等量代换解答；
（3）根据两点间垂直距离最短解答；

解答：（1）AM=AN．
证明：∵△ABC、△ACD、△AEF都是等边三角形，
∴∠BAE+∠EAC=∠CAN+∠EAC=60°，
∴∠BAE=∠CAN．
又∵AB=AC，∠B=∠ACN，
∴△ACN≌△ABM，
∴AM=AN．

（2）解：由（1）得，△ACN≌△ABM，
∴S_△ABM+S_△AMC=S_△ACN+S_△AMC=S_{四边形AMCN}，
又∵S_△ABM+S_△AMC=S_△ABC=

1

2

×12×12×sin60°=36

3

，
∴S_△ABC=S_{四边形AMCN}=36

3

，
∴四边形AMCN的面积是36

3

．

（3）解：∵△AEF是等边三角形，
∴∠EAF=60°，
∴S_△AMN=

1

2

AN•AM•sin60°，
∴只要AN、AM取最小值，S_△AMN就最小，
∵两点间的垂直距离最短，
∴当AN⊥CD、AM⊥BC时，△AMN面积最小．
在△ABM中，AM=12×sin60°=6

3

，
在△ANC中，AN=12×sin60°=6

3

，
∴S_△AMN=

1

2

AM•ANsin60°=27

3

，
∴当AN⊥CD、AM⊥BC时，△AMN面积最小，△AMN的最小面积是27

3

．

点评：解答本题的难点是全等三角形的判定．在突破难点时，充分利用等边三角形的性质：三条边相等，三个角相等且都是60°．