题目内容
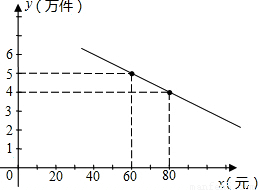
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着如图所示的一次函数关系.(1)求y关于x的函数关系式;
(2)试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?

【答案】分析:(1)设直线解析式为y=kx+b,把已知坐标代入求出k,b的值后可求出函数解析式;
(2)根据题意可知z=yx-40y-120,把x=100代入解析式即可;
(3)令z=40,代入解析式求出x的实际值.
解答: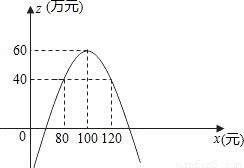 解:(1)设y=kx+b,它过点(60,5),(80,4),
解:(1)设y=kx+b,它过点(60,5),(80,4),
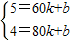 ,
,
解得: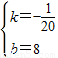 ,(2分)
,(2分)
∴y=-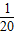 x+8;(3分)
x+8;(3分)
(2)z=yx-40y-120=(-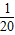 x+8)(x-40)-120=-
x+8)(x-40)-120=-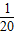 x2+10x-440
x2+10x-440
∴当x=100元时,最大年获利为60万元;(6分)
(3)令z=40,得40=-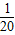 x2+10x-440,
x2+10x-440,
整理得:x2-200x+9600=0,
解得:x1=80,x2=120,(8分)
由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间,(9分)
又因为销售单价越低,销售量越大,
所以要使销售量最大,且年获利不低于40万元,销售单价应定为80元.(10分)
点评:本题考查的是二次函数的实际应用.考生应学会数形结合解答二次函数的相关题型.
(2)根据题意可知z=yx-40y-120,把x=100代入解析式即可;
(3)令z=40,代入解析式求出x的实际值.
解答:
 解:(1)设y=kx+b,它过点(60,5),(80,4),
解:(1)设y=kx+b,它过点(60,5),(80,4),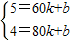 ,
,解得:
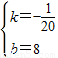 ,(2分)
,(2分)∴y=-
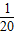 x+8;(3分)
x+8;(3分)(2)z=yx-40y-120=(-
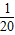 x+8)(x-40)-120=-
x+8)(x-40)-120=-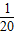 x2+10x-440
x2+10x-440∴当x=100元时,最大年获利为60万元;(6分)
(3)令z=40,得40=-
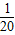 x2+10x-440,
x2+10x-440,整理得:x2-200x+9600=0,
解得:x1=80,x2=120,(8分)
由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间,(9分)
又因为销售单价越低,销售量越大,
所以要使销售量最大,且年获利不低于40万元,销售单价应定为80元.(10分)
点评:本题考查的是二次函数的实际应用.考生应学会数形结合解答二次函数的相关题型.

练习册系列答案
相关题目
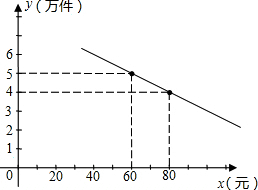 你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?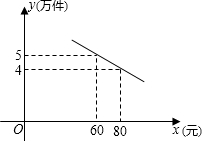 售量y(万件)与销售单价x(元)之间存在如图所示的一次函数关系.
售量y(万件)与销售单价x(元)之间存在如图所示的一次函数关系.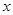 元.(
元.(