题目内容
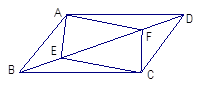
如图,在梯形ABCD中,AD∥BC,E是BC上的一点,且CE=8,BC=12,CD=4 ,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
(1)当x为何值时,以点P、A、D、E为顶点的四边形为直角梯形。
(2)当x为何值时,以点P、A、D、E为顶点的四边形为平行四边形。
(3)P在BC 上运动时,以点P、A、D、E为顶点的四边形能否为菱形。
 ,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。(1)当x为何值时,以点P、A、D、E为顶点的四边形为直角梯形。
(2)当x为何值时,以点P、A、D、E为顶点的四边形为平行四边形。
(3)P在BC 上运动时,以点P、A、D、E为顶点的四边形能否为菱形。

作AF垂直于BC于点F, DG垂直于BC于点G
∴DG=2 ,CG=6
,CG=6
∴DG=AF=2
∵∠B=60°
∴BF=2。
∵BC=12
∴FG=AD=4
显然,当P点与F或点G重合时,以点P、A、D、E为顶点的四边形为直角梯形。
所以x=2或x=6
(2)∵AD=BE=4,且AD∥BE
∴当点P与B重合时,
即x=0时。点P、A、D、E为顶点的四边形为平行四边形
又∵当点P在CE中点时,EP=AD=4,且EP∥AD,
∴x=8时,点P、A、D、E为顶点的四边形为平行四边形
(3)由(1)(2)知,∵∠BAF=30°
∴AB=2BF=4 所以当P与B重合时即x=0时或当x=8时点P、A、D、E为顶点的四边形为菱形
∴DG=2
 ,CG=6
,CG=6∴DG=AF=2

∵∠B=60°
∴BF=2。
∵BC=12
∴FG=AD=4
显然,当P点与F或点G重合时,以点P、A、D、E为顶点的四边形为直角梯形。
所以x=2或x=6
(2)∵AD=BE=4,且AD∥BE
∴当点P与B重合时,
即x=0时。点P、A、D、E为顶点的四边形为平行四边形
又∵当点P在CE中点时,EP=AD=4,且EP∥AD,
∴x=8时,点P、A、D、E为顶点的四边形为平行四边形
(3)由(1)(2)知,∵∠BAF=30°
∴AB=2BF=4 所以当P与B重合时即x=0时或当x=8时点P、A、D、E为顶点的四边形为菱形
(1)如图,分别过A、D作BC的垂线,垂足分别为F、G,容易得到AF=DG,AD=FG,而CD=4 ,∠C=30°,由此可以求出CG=6,DG=AF=2
,∠C=30°,由此可以求出CG=6,DG=AF=2 ,又∠B=60°,BF=2,若点P、A、D、E为顶点的四边形为直角梯形,则∠APC=90°或∠DPC=90°,那么P与F重合或P与G重合,根据前面求出的长度即可求出此时的x的值;
,又∠B=60°,BF=2,若点P、A、D、E为顶点的四边形为直角梯形,则∠APC=90°或∠DPC=90°,那么P与F重合或P与G重合,根据前面求出的长度即可求出此时的x的值;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,由于AD=BE=4,且AD∥BE,有两种情况:①当点P与B重合时,利用已知条件可以求出BP的长度;②当点P在CE中点时,利用已知条件也可求出BP的长度;
(3)以点P、A、D、E为顶点的四边形能构成菱形.由(1)(2)知,当BP=0或8时,以点P、A、D、E为顶点的四边形是平行四边形,根据已知条件分别计算一组邻边证明它们相等即可证明它是菱形.
 ,∠C=30°,由此可以求出CG=6,DG=AF=2
,∠C=30°,由此可以求出CG=6,DG=AF=2 ,又∠B=60°,BF=2,若点P、A、D、E为顶点的四边形为直角梯形,则∠APC=90°或∠DPC=90°,那么P与F重合或P与G重合,根据前面求出的长度即可求出此时的x的值;
,又∠B=60°,BF=2,若点P、A、D、E为顶点的四边形为直角梯形,则∠APC=90°或∠DPC=90°,那么P与F重合或P与G重合,根据前面求出的长度即可求出此时的x的值;(2)若以点P、A、D、E为顶点的四边形为平行四边形,由于AD=BE=4,且AD∥BE,有两种情况:①当点P与B重合时,利用已知条件可以求出BP的长度;②当点P在CE中点时,利用已知条件也可求出BP的长度;
(3)以点P、A、D、E为顶点的四边形能构成菱形.由(1)(2)知,当BP=0或8时,以点P、A、D、E为顶点的四边形是平行四边形,根据已知条件分别计算一组邻边证明它们相等即可证明它是菱形.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目



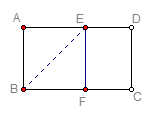

 于E,
于E, 于F,BD与AE、AF分别相交于G、H.
于F,BD与AE、AF分别相交于G、H. ,求证:四边形ABCD是菱形.
,求证:四边形ABCD是菱形.
 相交于点
相交于点 ,
, ,若要使□ABCD为矩形,则
,若要使□ABCD为矩形,则 的长应该为( ).
的长应该为( ).