题目内容
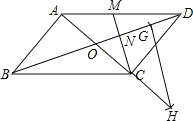
【题目】如图,在平四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
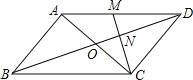
(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
【答案】(1)6;(2)见解析
【解析】
试题分析:(1)根据平行四边形的性质得AD∥BC,AD=BC,OB=OD,则利用DM∥BC可判断△MND∽△CNB,所以MD:BC=DN:BN=1:2,设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x﹣1,于是得到x+1=2(x﹣1),解得x=3,所以BD=2x=6;
(2)如图,在OD上截取NG=ON,延长OC到H,使HC=OC,则△HOG满足条件.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴DM∥BC,
∴△MND∽△CNB,
∴MD:BC=DN:BN,
∵M为AD中点,
∴MD:BC=1:2,
∴DN:BN=1:2,即BN=2DN,
设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x﹣1,
∴x+1=2(x﹣1),解得x=3,
∴BD=2x=6;
(2)如图,△HOG为所作.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.