Question

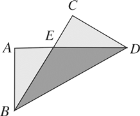
【题目】如图，在 Rt△ABC 中，∠BAC＝90°，AD⊥BC 于 D，BE 平分∠ABC 交 AC 于 E， 交 AD 于 F，FG∥BC，FH∥AC，下列结论：①AE＝AF；②ΔABF≌ΔHBF；③AG＝CE；④AB＋FG＝BC，其中正确的结论有（）

A.①②③B.①③④C.①②③④D.①②④

Answer 1

【答案】C

【解析】

只要证明∠AFE=∠AEF，四边形FGCH是平行四边形，△FBA≌△FBH即可解决问题；

解：∵∠FBD=∠ABF，∠FBD+∠BFD=90°，∠ABF+∠AEB=90°，

∴∠BFD=∠AEB，

∴∠AFE=∠AEB，

∴AF=AE，故①正确，

∵FG∥BC，FH∥AC，

∴四边形FGCH是平行四边形，

∴FH=CG，FG=CH，∠FHD=∠C，

∵∠BAD+∠DAC=90°，∠DAC+∠C=90°，

∴∠BAF=∠BHF，

∵BF=BF，∠FBA=∠FBH，

∴△FBA≌△FBH，

∴FA=FH，故AB=BH，②正确，

∵AF=AE，FH=CG，

∴AE=CG，

∴AG=CE，故③正确，

∵BC=BH+HC，BH=BA，CH=FG，

∴BC=AB+FG，故④正确．

故选C．