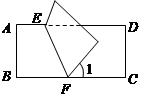题目内容
如图,在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,∠AOB=45°,则∠BAE的大小为( ).
A.15° B.45° C.30° D.22.5°
D
解析试题分析:根据同角的余角相等易证∠BAE=∠ADE,根据矩形对角线相等且互相平分的性质,可得∠OAB=∠OBA,在Rt△ABD中,已知∠OBA即可求得∠ADB的大小,从而得到结果.
∵∠BAE+∠ABD=90°,∠ADE+∠ABD=90°,
∴∠BAE=∠ADE
∵矩形对角线相等且互相平分
∴∠OAB=∠OBA=(180°-45°)÷2=67.5°,
∴∠BAE=∠ADE=90-67.5°=22.5°,
故选D.
考点:矩形的性质
点评:特殊四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
如果∠AOB+∠BOC=90°,且∠BOC与∠COD互余,那么∠AOB与∠COD的关系为( )
| A.互余 | B.互补 | C.互余或互补 | D.相等 |
如图,已知直线a∥b,∠1=1310,则∠2等于【 】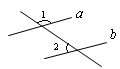
| A.390 | B.410 | C.490 | D.590 |