题目内容
【题目】请把下列证明过程补充完整.已知:如图，B、C、E三点在同一直线上，A、F、E三点在同一直线上，∠1=∠2=∠E，∠3=∠4.求证:AB∥CD.
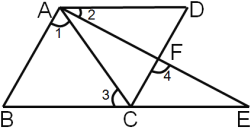
证明:∵∠2=∠E(已知)
∴ ∥BC( )
∴∠3=∠ ( )
∵∠3=∠4(已知)
∴∠4=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF ，即∠BAF=∠
∴∠4=∠ (等量代换)
∴ ( )
【答案】见解析
【解析】根据平行线的判定可得AD∥BC，根据平行线的性质和等量关系可得∠4=∠BAC，再根据平行线的判定可得AB∥CD．
详证明：∵∠2=∠E（已知）
∴AD∥BC（ 内错角相等，两直线平行）
∴∠3=∠DAC（ 两直线平行，内错角相等）
∵∠3=∠4（已知）
∴∠4=∠DAC（ 等量关系）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF
即∠BAF=∠DAC
∴∠4=∠BAC（等量代换）
∴AB∥CD（ 同位角相等，两直线平行）
故答案为：AD，内错角相等，两直线平行；DAC，两直线平行，内错角相等；DAC，等量关系；DAC，BAC；AB∥CD，同位角相等，两直线平行．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
【题目】下表是今年雨季某河流一周的水位变化情况(上周末的水位达到警戒水位)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位记录 |
|
|
|
|
|
|
|
注:此河流的警戒水位为
米．
完成下面的本周水位变化记录表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
|
|
|
(注:规定水位比前一天上升用“
”，水位比前一天下降用“
”，不升不降记作“
”．)
与上周末相比，本周末河流水位是上升了还是下降了? (填“上升”或“下降”)
