题目内容
【题目】在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)

(1)小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.
请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是 三角形;∠ADB的度数为 .
(2)在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;
(3)在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC=7,AD=2.请直接写出线段BE的长为 .
【答案】(1)①△D′BC是等边三角形,②∠ADB=30°(2)∠ADB=30°;(3)7+![]() 或7﹣
或7﹣![]()
【解析】
(1)①如图2中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,由△ABD≌△ABD′,推出△D′BC是等边三角形;
②借助①的结论,再判断出△AD′B≌△AD′C,得∠AD′B=∠AD′C,由此即可解决问题.
(2)当60°<α≤120°时,如图3中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,证明方法类似(1).
(3)第①种情况:当60°<α≤120°时,如图3中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,证明方法类似(1),最后利用含30度角的直角三角形求出DE,即可得出结论;第②种情况:当0°<α<60°时,如图4中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.证明方法类似(1),最后利用含30度角的直角三角形的性质即可得出结论.
(1)①如图2中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,

∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵∠DBC=30°,
∴∠ABD=∠ABC﹣∠DBC=15°,
在△ABD和△ABD′中,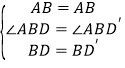
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
②∵△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
在△AD′B和△AD′C中,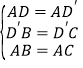
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=![]() ∠BD′C=30°,
∠BD′C=30°,
∴∠ADB=30°.
(2)∵∠DBC<∠ABC,
∴60°<α≤120°,
如图3中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,
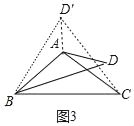
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∴∠ABD=∠ABC﹣∠DBC=90°﹣![]() α﹣β,
α﹣β,
同(1)①可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°﹣![]() α﹣β,BD=BD′,∠ADB=∠AD′B
α﹣β,BD=BD′,∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=90°﹣![]() α﹣β+90°﹣
α﹣β+90°﹣![]() α=180°﹣(α+β),
α=180°﹣(α+β),
∵α+β=120°,
∴∠D′BC=60°,
由(1)②可知,△AD′B≌△AD′C,
<>∴∠AD′B=∠AD′C,∴∠AD′B=![]() ∠BD′C=30°,
∠BD′C=30°,
∴∠ADB=30°.
(3)第①情况:当60°<α<120°时,如图3﹣1,
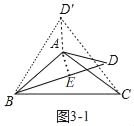
由(2)知,∠ADB=30°,
作AE⊥BD,
在Rt△ADE中,∠ADB=30°,AD=2,
∴DE=![]() ,
,
∵△BCD'是等边三角形,
∴BD'=BC=7,
∴BD=BD'=7,
∴BE=BD﹣DE=7﹣![]() ;
;
第②情况:当0°<α<60°时,
如图4中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.
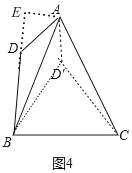
同理可得:∠ABC=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∴∠ABD=∠DBC﹣∠ABC=β﹣(90°﹣![]() α),
α),
同(1)①可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=β﹣(90°﹣![]() α),BD=BD′,∠ADB=∠AD′B,
α),BD=BD′,∠ADB=∠AD′B,
∴∠D′BC=∠ABC﹣∠ABD′=90°﹣![]() α﹣[β﹣(90°﹣
α﹣[β﹣(90°﹣![]() α)]=180°﹣(α+β),
α)]=180°﹣(α+β),
∴D′B=D′C,∠BD′C=60°.
同(1)②可证△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°,
在Rt△ADE中,∠ADE=30°,AD=2,
∴DE=![]() ,
,
∴BE=BD+DE=7+![]() ,
,
故答案为:7+![]() 或7﹣
或7﹣![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案