题目内容
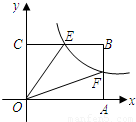
(2008•兰州)如图,已知双曲线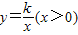 )经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .
)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .
【答案】分析:如果设F(x,y),表示点B坐标,再根据四边形OEBF的面积为2,列出方程,从而求出k的值.
解答: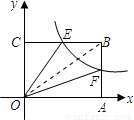 解:设F(x,y),那么B(x,2y),
解:设F(x,y),那么B(x,2y),
∵E在反比例函数解析式上,
∴S△COE= k,
k,
∵S四边形OEBF=S矩形ABCO-S△COE-S△AOF,且S四边形OEBF=2,
∴2xy- k-
k- xy=2,
xy=2,
2k- k-
k- k=2,
k=2,
∴k=2.
故本题答案为2.
点评:本题的难点是根据点F的坐标得到其他点的坐标.在反比例函数上的点的横纵坐标的积等于反比例函数的比例系数.
解答:
 解:设F(x,y),那么B(x,2y),
解:设F(x,y),那么B(x,2y),∵E在反比例函数解析式上,
∴S△COE=
 k,
k,∵S四边形OEBF=S矩形ABCO-S△COE-S△AOF,且S四边形OEBF=2,
∴2xy-
 k-
k- xy=2,
xy=2,2k-
 k-
k- k=2,
k=2,∴k=2.
故本题答案为2.
点评:本题的难点是根据点F的坐标得到其他点的坐标.在反比例函数上的点的横纵坐标的积等于反比例函数的比例系数.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
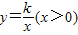 )经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .
)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .
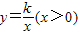 )经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .
)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .
 )经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .
)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .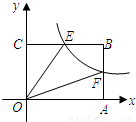
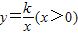 )经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .
)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k= .