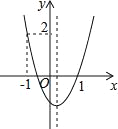��Ŀ����
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P�͡�C���������¶��壺����C�ϴ���һ����M��ʹ��MP��MC����Ƶ�PΪ��C�ġ��Ⱦ��㡱����֪��D��![]() ��
��![]() ����E��0��2
����E��0��2![]() ����F����2��0����
����F����2��0����
��1������O�İ뾶Ϊ1ʱ��
���ڵ�D��E��F�У���O�ġ��Ⱦ��㡱���ļ����㣻
����ֱ��EF����ֱ��EF�ϵĵ�T��m��n���ǡ�O�ġ��Ⱦ��㡱����m��ȡֵ��Χ��
��2������E��EG��EF��x���ڵ�G������EFG���������еĵ㶼��ij��Բ�ġ��Ⱦ��㡱�������Բ�İ뾶r��ȡֵ��Χ��
���𰸡���1���١�O�ġ��Ⱦ��㡱��D��E���ک�2��m�ܩ�1����2�����Բ�İ뾶r��ȡֵ��ΧΪr��2��
��������
��1���ٸ��ݡ��Ⱦ��㡱�Ķ����֪�����Ⱦ��㡱��Բ�ĵľ���С�ڵ���Բ�İ뾶��2�����ɴ˼����ж���
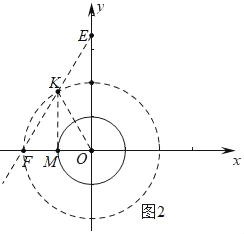
����ͼ2�У���ֱ��EF���뾶Ϊ2�ġ�O�ڵ�K������OK����KM��OF��M������T���߶�FK��ʱ����T�ǡ��Ⱦ��㡱�������K�����꼴�ɽ�����⣻
��2����Ϊ��EFG���������еĵ㶼��ij��Բ�ġ��Ⱦ��㡱���������Բ��Բ��Q���߶�FG���е㣬��֪Q��2��0���������Բ�İ뾶Ϊr������QG��2r����������ʽ���ɽ������.
��1�����ݡ��Ⱦ��㡱�Ķ����֪�����Ⱦ��㡱��Բ�ĵľ���С�ڵ���Բ�İ뾶��2�������뾶Ϊ1�ġ�O�ġ��Ⱦ��㡱����OΪԲ��2Ϊ�뾶��Բ�ڻ�Բ�ϣ�
��ͼ1�У��۲�ͼ���֪���ڵ�D��E��F�У���O�ġ��Ⱦ��㡱��D��E��
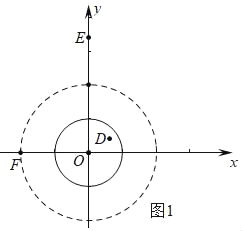
����ͼ2�У���ֱ��EF���뾶Ϊ2�ġ�O�ڵ�K������OK����KM��OF��M��
��OF��2��OE��2![]() ��
��
��tan��EFO��![]() =
=![]() ��
��
���OFK��60�㣬
��OF��OK��
���OFK�ǵȱ������Σ�
��OF��OK��FK��2��
��KM��OF��
��FM��OM��1��KM��![]() ��
��![]() ��
��
��K����1��![]() ����
����
�ߵ���T���߶�FK��ʱ����T�ǡ��Ⱦ��㡱��
�ੁ2��m�ܩ�1��
��2����ͼ3�У�
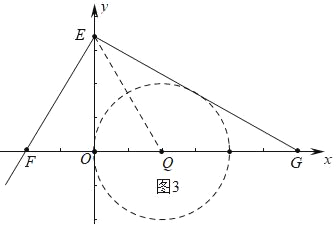
�ߡ�EFG��ֱ�������Σ���FEG��90�㣬��EFG��60�㣬
��EF��2OF��4��FG��2EF��8��
��OG��6��
�������EFG���������еĵ㶼��ij��Բ�ġ��Ⱦ��㡱�����Բ��Բ��Q���߶�FG���е㣬Q��2��0���������Բ�İ뾶Ϊr��
�����⣺QG��2r
��4��2r��
��r��2��
�����Բ�İ뾶r��ȡֵ��ΧΪr��2��

 ͬ����ϰ����ʦ����ѧ������ϵ�д�
ͬ����ϰ����ʦ����ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�