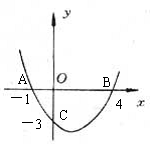
题目内容
已知二次函数y=ax2的图象经过点A(
,
)、B(3,m).
(1)求a与m的值;
(2)当-2<x<4时,函数值y的取值范围.
(3)写出将其图象向下平移4个单位、再向左平移2个单位后的解析式.
| 1 |
| 2 |
| 1 |
| 8 |
(1)求a与m的值;
(2)当-2<x<4时,函数值y的取值范围.
(3)写出将其图象向下平移4个单位、再向左平移2个单位后的解析式.
分析:(1)把点A坐标代入函数解析式求出a的值,从而得到二次函数解析式,再把点B坐标代入求出m的值即可;
(2)根据二次函数的增减性求出x=4和x=0时的值,然后写出y的取值范围即可;
(3)根据向下平移纵坐标减,向左平移横坐标减求出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出即可.
(2)根据二次函数的增减性求出x=4和x=0时的值,然后写出y的取值范围即可;
(3)根据向下平移纵坐标减,向左平移横坐标减求出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出即可.
解答:解:(1)把A(
,
)代入y=ax2得,
a×(
)2=
,
解得a=
,
所以,二次函数的解析式为y=
x2,
把B(3,m)代入函数解析式得,m=
×32=
;
(2)x=4时,y=
×42=8,
x=0时,y=0,
所以,当-2<x<4时,函数值y的取值范围0<y<8;
(3)∵图象向下平移4个单位、再向左平移2个单位,
∴平移后的函数图象顶点坐标为(-2,-4),
∴平移后的函数解析式为y=
(x+2)2-4.
| 1 |
| 2 |
| 1 |
| 8 |
a×(
| 1 |
| 2 |
| 1 |
| 8 |
解得a=
| 1 |
| 2 |
所以,二次函数的解析式为y=
| 1 |
| 2 |
把B(3,m)代入函数解析式得,m=
| 1 |
| 2 |
| 9 |
| 2 |
(2)x=4时,y=
| 1 |
| 2 |
x=0时,y=0,
所以,当-2<x<4时,函数值y的取值范围0<y<8;
(3)∵图象向下平移4个单位、再向左平移2个单位,
∴平移后的函数图象顶点坐标为(-2,-4),
∴平移后的函数解析式为y=
| 1 |
| 2 |
点评:本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征,主要利用了二次函数的对称性,以及平移的规律:左加右减,上加下减.

练习册系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
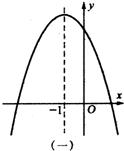 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )