题目内容
 如图,一块直角三角形铁板被一块大铁板压在地面上,AB∥CD,已知CD=20,AB=30,BC=10,求直角三角形铁板被大铁板压住部分的面积.
如图,一块直角三角形铁板被一块大铁板压在地面上,AB∥CD,已知CD=20,AB=30,BC=10,求直角三角形铁板被大铁板压住部分的面积.
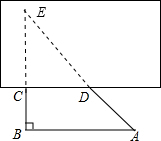 解:延长AD,BC交于点E,
解:延长AD,BC交于点E,∵CD∥AB,
∴△ECD∽△EBA,
∴
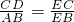 ,
,∵CD=20,AB=30,BC=10,
∴EC=20,
∴S△ECD=
 ×CD•CE=200,
×CD•CE=200,答:直角三角形铁板被大铁板压住部分的面积是200.
分析:延长AD,BC交于点E,证出△ECD∽△EBA利用相似三角形的性质:对应边的比值相等即可求出CE的长,利用三角形的面积公式可求出直角三角形铁板被大铁板压住部分的面积.
点评:本题考查了相似三角形的判定和性质以及三角形的面积公式的运用,题目的难度不大,但设计很新颖.

练习册系列答案
相关题目
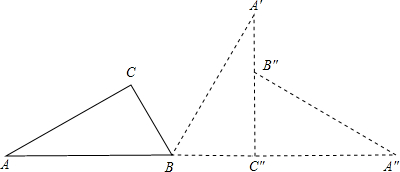

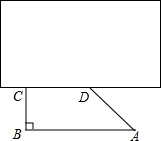 如图,一块直角三角形铁板被一块大铁板压在地面上,AB∥CD,已知CD=20,AB=30,BC=10,求直角三角形铁板被大铁板压住部分的面积.
如图,一块直角三角形铁板被一块大铁板压在地面上,AB∥CD,已知CD=20,AB=30,BC=10,求直角三角形铁板被大铁板压住部分的面积. 如图有一块直角三角形纸片,∠A=30°,BC=
如图有一块直角三角形纸片,∠A=30°,BC= 如图在一块直角三角形地被分成BD分成两块,其中斜边AB长为13m,一条直角边BC长为
如图在一块直角三角形地被分成BD分成两块,其中斜边AB长为13m,一条直角边BC长为