题目内容
如图,平面直角坐标系中,以点C(2, )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
解:(1)如图,过点C作CM⊥x轴于点M,则MA=MB,连接AC,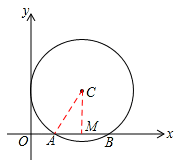
∵点C的坐标为(2, ),∴OM=2,CM=
),∴OM=2,CM= 。
。
在Rt△ACM中,CA=2,∴ 。
。
∴OA=OM﹣AM=1,OB=OM+BM=3。
∴A点坐标为(1,0),B点坐标为(3,0)。
(2)将A(1,0),B(3,0)代入y=x2+bx+c得 ,解得
,解得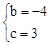 。
。
∴二次函数的解析式为y=x2﹣4x+3。
解析试题分析:(1)连接AC,过点C作CM⊥x轴于点M,根据垂径定理得MA=MB;由C点坐标得到OM=2,CM=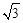 ,再根据勾股定理可计算出AM,可可计算出OA、OB,然后写出A,B两点的坐标。
,再根据勾股定理可计算出AM,可可计算出OA、OB,然后写出A,B两点的坐标。
(2)利用待定系数法求二次函数的解析式。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知反比例函数的图象 上有两点A(x1,y1)、B(x2,y2),若y1>y2,则x1-x2的值是( )
上有两点A(x1,y1)、B(x2,y2),若y1>y2,则x1-x2的值是( )
| A.正数 | B.负数 | C.非正数 | D.不能确定 |
 交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.


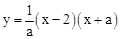 (a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.

 经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
 交y轴于点A,交x轴正半轴于点B.
交y轴于点A,交x轴正半轴于点B.