题目内容
 如图所示,学校正在食堂旁边建一栋教师公寓总共5层,建好后再其前面和⑤栋之间建一灯光球场,教师还可以在上面打太极,如图宽21m,长27m的矩形,正中央是一个与整个球场长宽比例相同的矩形,如果要使四周的观众区所占面积是整个球场面积的四分之一,上、下观众区等宽,左、右边观众区等宽,应如何设计四周观众区的宽度(精确到0.1cm)?
如图所示,学校正在食堂旁边建一栋教师公寓总共5层,建好后再其前面和⑤栋之间建一灯光球场,教师还可以在上面打太极,如图宽21m,长27m的矩形,正中央是一个与整个球场长宽比例相同的矩形,如果要使四周的观众区所占面积是整个球场面积的四分之一,上、下观众区等宽,左、右边观众区等宽,应如何设计四周观众区的宽度(精确到0.1cm)?分析:设中央矩形的长与宽为9x米,7x米,根据面积关系建立方程和建立方程构成方程求出其解即可.
解答:解:设正中央矩形的宽为7x米,矩形的长为9x米,由题意,得
7x×9x=21×27×
,
解得:x=±
(-
舍去),
∴上下观众区宽为(21-7×
)÷2=(
-
)≈1.407米=140.7cm
左右观众区的宽度为(27-9×
)÷2=(
-
)≈1.809米=180.9cm.
7x×9x=21×27×
| 3 |
| 4 |
解得:x=±
3
| ||
| 2 |
3
| ||
| 2 |
∴上下观众区宽为(21-7×
3
| ||
| 2 |
| 21 |
| 2 |
21
| ||
| 4 |
左右观众区的宽度为(27-9×
3
| ||
| 2 |
| 27 |
| 2 |
27
| ||
| 4 |
点评:本题考查了矩形的面积公式的运用,列一元二次方程解实际问题的运用,求近似数的方法的运用,解答时由矩形的面积关系建立方程是关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目

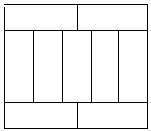 如图所示,学校为了提高绿化品位、美化环境,准备将一块周长为76米的长方形草地设计分成形状大小完全相同的九块长方形,种上各种花卉.经市场预测,牡丹花每平方米造价150元,玫瑰花每平方米造价135元,茉莉花每平方米造价130元.
如图所示,学校为了提高绿化品位、美化环境,准备将一块周长为76米的长方形草地设计分成形状大小完全相同的九块长方形,种上各种花卉.经市场预测,牡丹花每平方米造价150元,玫瑰花每平方米造价135元,茉莉花每平方米造价130元. 22、如图所示,学校准备在教学楼后面搭建一个面积为150m2的简易自行车车棚,一边利用教学楼的后墙(可利用的墙长为18m),另外三边利用学校现有的总长35m的铁围栏围成,试求出自行车车棚的长和宽.
22、如图所示,学校准备在教学楼后面搭建一个面积为150m2的简易自行车车棚,一边利用教学楼的后墙(可利用的墙长为18m),另外三边利用学校现有的总长35m的铁围栏围成,试求出自行车车棚的长和宽. 如图所示,学校正在食堂旁边建一栋教师公寓总共5层,建好后再其前面和⑤栋之间建一灯光球场,教师还可以在上面打太极,如图宽21m,长27m的矩形,正中央是一个与整个球场长宽比例相同的矩形,如果要使四周的观众区所占面积是整个球场面积的四分之一,上、下观众区等宽,左、右边观众区等宽,应如何设计四周观众区的宽度(精确到0.1cm)?
如图所示,学校正在食堂旁边建一栋教师公寓总共5层,建好后再其前面和⑤栋之间建一灯光球场,教师还可以在上面打太极,如图宽21m,长27m的矩形,正中央是一个与整个球场长宽比例相同的矩形,如果要使四周的观众区所占面积是整个球场面积的四分之一,上、下观众区等宽,左、右边观众区等宽,应如何设计四周观众区的宽度(精确到0.1cm)?