��Ŀ����
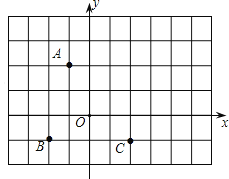
����Ŀ�����������֣���ͼ1��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�![]() ���Ƚ����ǰ��
���Ƚ����ǰ��![]() ����
����![]() �غϣ��ٽ����ǰ��Ƶ�
�غϣ��ٽ����ǰ��Ƶ�![]() ��˳ʱ�뷽����ת����ת�Ǵ���
��˳ʱ�뷽����ת����ת�Ǵ���![]() ��С��
��С��![]() ������ת�����ǰ��һֱ�DZ���
������ת�����ǰ��һֱ�DZ���![]() ���ڵ�
���ڵ�![]() �������ǰ���һֱ�DZ���ȡһ��
�������ǰ���һֱ�DZ���ȡһ��![]() ��ʹ
��ʹ![]() ���߶�
���߶�![]() ��ȡ��
��ȡ��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��![]() ��
��

��1�������![]() �Ķ�����
�Ķ�����
��2��![]() ��
��![]() �������˵�����ɣ�
�������˵�����ɣ�
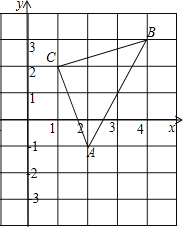
�����̽������ͼ2��![]() Ϊ�ȱ������Σ��Ƚ����ǰ��е�
Ϊ�ȱ������Σ��Ƚ����ǰ��е�![]() ����
����![]() �غϣ��ٽ����ǰ��Ƶ�
�غϣ��ٽ����ǰ��Ƶ�![]() ��˳ʱ�뷽����ת����ת�Ǵ���
��˳ʱ�뷽����ת����ת�Ǵ���![]() ��С��
��С��![]() ��.��ת�����ǰ��һֱ�DZ���
��.��ת�����ǰ��һֱ�DZ���![]() ���ڵ�
���ڵ�![]() .�����ǰ�б����ȡһ��
.�����ǰ�б����ȡһ��![]() ��ʹ
��ʹ![]() ���߶�
���߶�![]() ��ȡ��
��ȡ��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��![]() .
.
��3��ֱ��д��![]() _________�ȣ�
_________�ȣ�
��4����![]() ��
��![]() �����߶�
�����߶�![]() �ij���.
�ij���.
���𰸡���1��![]() ����2����ȣ����������������3��
����2����ȣ����������������3��![]() ����4��
����4��![]()
��������
��1������ȫ�������ε��ж��ó�![]() ������ȫ�������ε����ʵõ�
������ȫ�������ε����ʵõ�![]() ��
��![]() ��Ȼ����ݵ��������ε��ж������ʼ��ɵý⣻
��Ȼ����ݵ��������ε��ж������ʼ��ɵý⣻
��2������ȫ�������ε��ж��ó�![]() ������ȫ�������ε����ʵ�֤���ۣ�
������ȫ�������ε����ʵ�֤���ۣ�
��3������ȫ�������ε��ж��ó�![]() ������ȫ�������ε����ʵõ�
������ȫ�������ε����ʵõ�![]() ��
��![]() ��Ȼ����ݵȱ������ε��ж������ʼ��ɵý⣻
��Ȼ����ݵȱ������ε��ж������ʼ��ɵý⣻
��4������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() �������
�������![]() �����ú�
�����ú�![]() �ǵ�ֱ�������ε��������
�ǵ�ֱ�������ε��������![]() ���ٸ��ݹ��ɶ������
���ٸ��ݹ��ɶ������![]() ������ɹ��ɶ���������ô𰸣�
������ɹ��ɶ���������ô𰸣�
�⣺��1����![]() Ϊ����ֱ�������Σ���
Ϊ����ֱ�������Σ���![]()
��![]() ��
��![]()
��![]()
��![]()
��![]()
��![]() ��
��![]() ��
�У�
��![]()
��![]() ��
��![]()
��![]() ��
��
��2����ȣ��������£�
��![]() ��
��![]()
��![]()
��![]()
��![]() ��
��![]() ��
�У�
��![]()
�� ![]() ��
��
��3����![]() Ϊ�ȱ�������
Ϊ�ȱ�������
��![]() ��
��![]()
��![]()
��![]()
��![]()
��![]() ��
��![]() ��
�У�
��![]()
��![]()
��![]() ��
��
��4������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ����ͼ��
����ͼ��

���ɣ�3����֪��![]() ��
��![]()
��![]() ��
��![]()
��![]()
��![]()
��![]() ��
��![]()
��![]() ��
��

����Ŀ��Ϊ�˽�ijУѧ���ԡ���ǿ���ԡ������ʶ��ߡ������й�ʫ�ʴ�ᡷ���������й��ˡ��ĸ����ӽ�Ŀ��ϲ������������ȡ��![]() ��ѧ�����е���ͳ�ƣ�Ҫ��ÿ��ѧ��ѡ������ֻ��ѡ��һ���Լ���ϲ���Ľ�Ŀ�����������������Ƴ�����ͳ��ͼ��:
��ѧ�����е���ͳ�ƣ�Ҫ��ÿ��ѧ��ѡ������ֻ��ѡ��һ���Լ���ϲ���Ľ�Ŀ�����������������Ƴ�����ͳ��ͼ��:

ѧ����ϲ���Ľ�Ŀ��������ͳ��ͼ
��Ŀ | ����( �� ) | �ٷֱ� |
��ǿ���� | 5 | 10% |
�ʶ��� | 15 |
|
�й�ʫ�ʴ�� |
| 40% |
������� | 10 | 20% |
ѧ����ϲ���Ľ�Ŀ����ͳ�Ʊ�
���������ṩ����Ϣ�������������:
��1��![]() =
= ![]() =
= ![]() = ��
= ��
��2����ȫ����ͳ��ͼ��
��3������У����ѧ��1200�������ݳ��������������Ƹ�У��ϲ�����й�ʫ�ʴ�ᡷ��Ŀ��ѧ���ж�������